蒙特卡洛模拟
蒙特卡洛模拟通常用于建模随机系统的行为。本用户指南的这一部分涵盖了使用数学表达式执行蒙特卡洛模拟的基础知识。
随机时间序列
股票价格的每日变动通常被描述为“随机游走”。但这到底意味着什么,它与随机时间序列有何不同?下面的示例将使用蒙特卡洛模拟来探索“随机游走”和随机时间序列。
理解差异的有用第一步是将每日股票回报(计算为收盘价减去开盘价)可视化为时间序列。
下面的示例使用 search 函数返回股票代码为 CVX(雪佛龙)的 1000 天的每日股票回报。然后将 change_d 字段(即当日价格变动)绘制为时间序列。
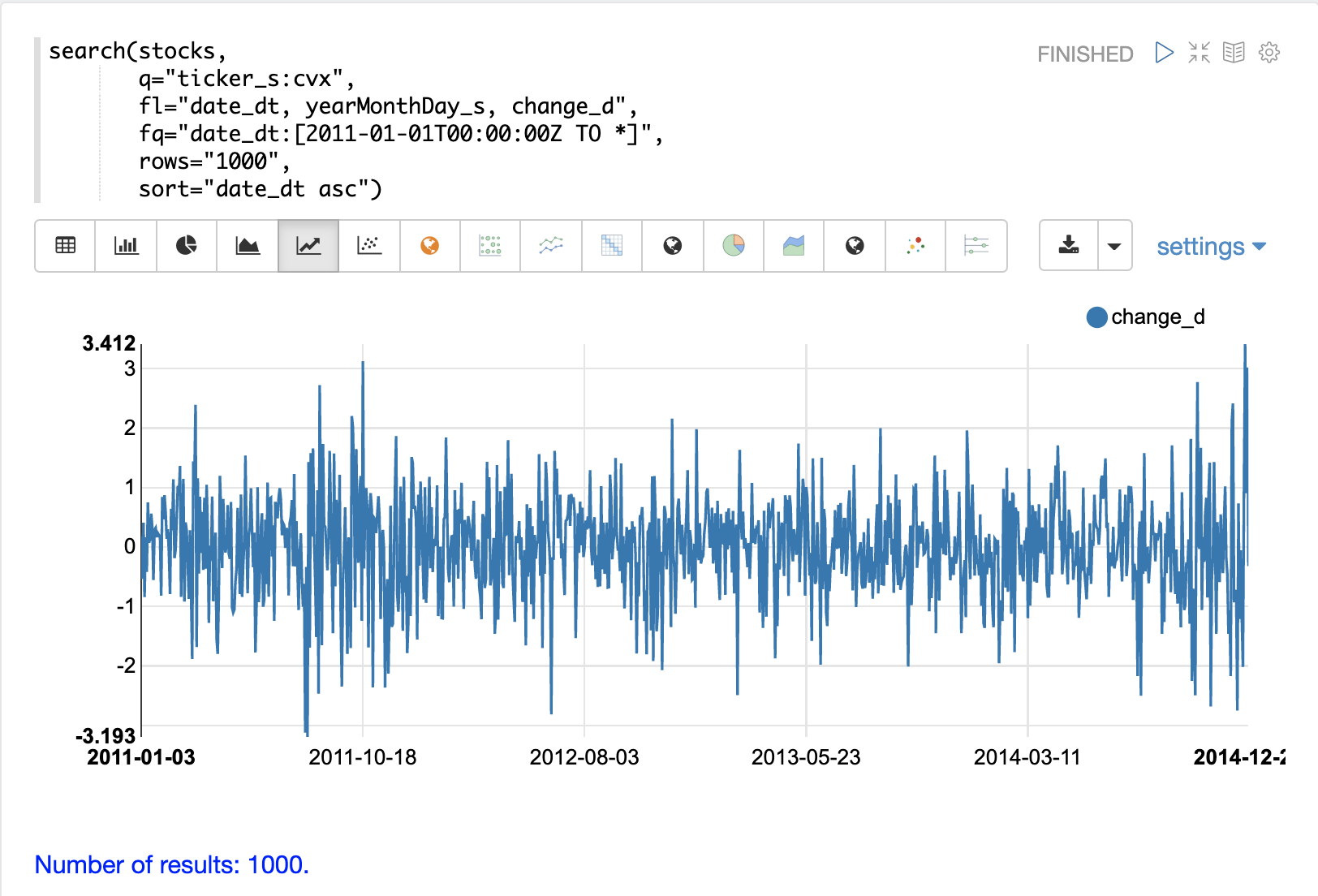
请注意,每日价格变化的时间序列在零上下随机波动。有时股票上涨,有时下跌,但似乎没有明显的模式或步骤之间的任何依赖关系。这暗示着这是一个**随机时间序列**。
自相关
自相关测量信号与其自身相关的程度。自相关可用于确定向量是否包含信号,或者时间序列中的值之间是否存在依赖关系。如果时间序列中没有信号并且值之间没有依赖关系,则时间序列是随机的。
绘制 change_d 向量的自相关来确认它确实是随机的很有用。
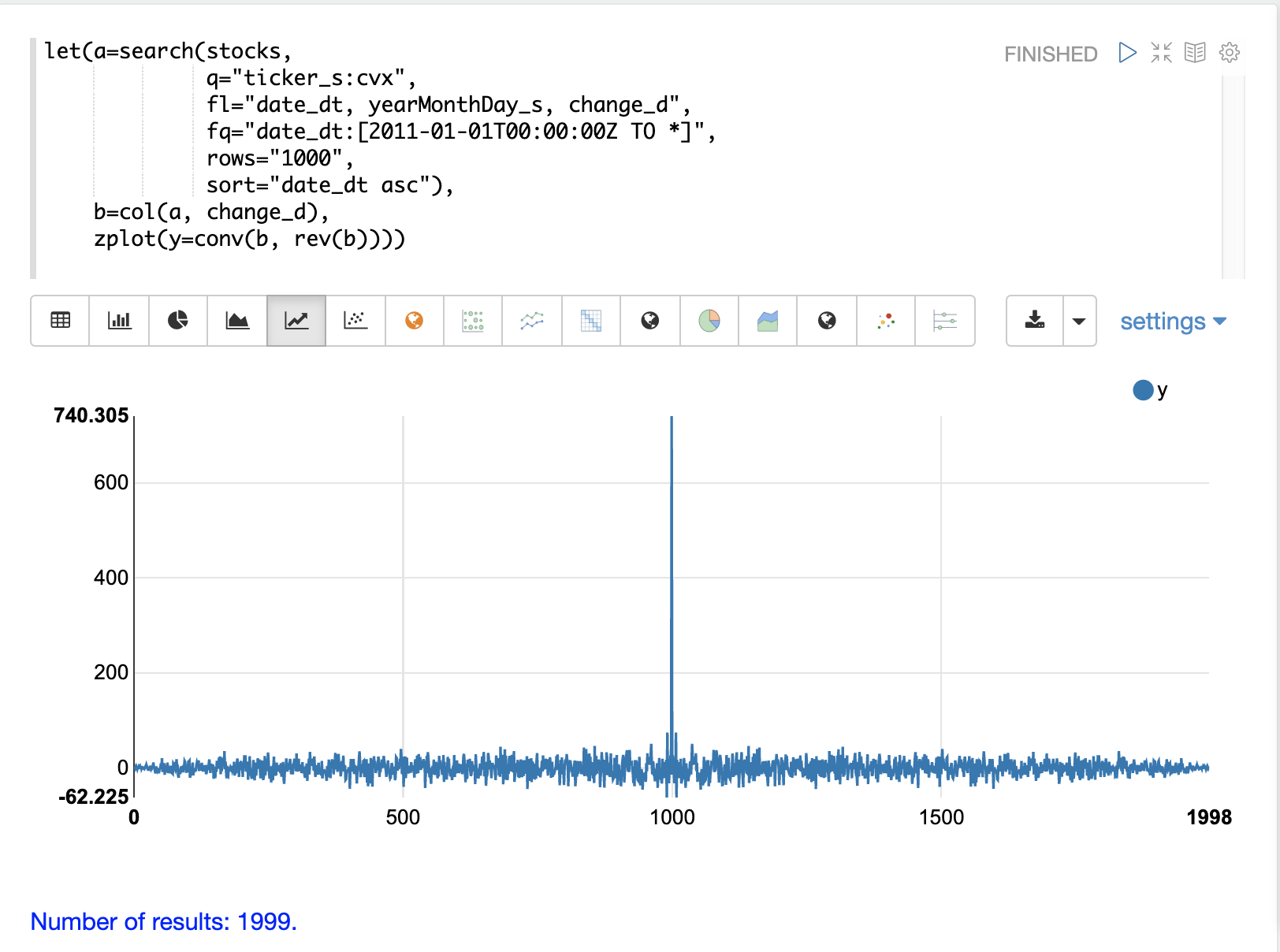
在下面的示例中,搜索结果被设置为一个变量,然后将 change_d 字段向量化并存储在变量 b 中。然后使用 conv(卷积)函数来自动关联 change_d 向量。请注意,conv 函数只是将 change_d 向量与其自身的反向副本进行“卷积”。这是使用卷积执行自相关的方法。用户指南的 数字信号处理 部分详细介绍了卷积和自相关。在本节中,我们将只讨论绘图。
该图显示了当 change_d 向量被 conv 函数滑过自身时计算的相关强度。请注意,在图中,存在很长一段低强度相关的时期,似乎是随机的。然后在中心出现一个高强度相关的峰值,其中向量直接对齐。之后是另一段较长的低强度相关时期。
这是纯噪声的自相关图。每日股票变化似乎是一个随机时间序列。
可视化分布
股票价格的每日随机变动是无法预测的,但可以使用概率分布进行建模。为了对时间序列进行建模,我们将首先可视化 change_d 向量的分布。在下面的示例中,使用 empiricalDistribution 函数绘制了 change_d 向量,以创建数据的 11 个箱子的直方图。请注意,该分布似乎呈正态分布。每日股票价格变化确实倾向于呈正态分布,尽管选择 CVX 作为此示例的特殊原因正是因为其具有此特征。
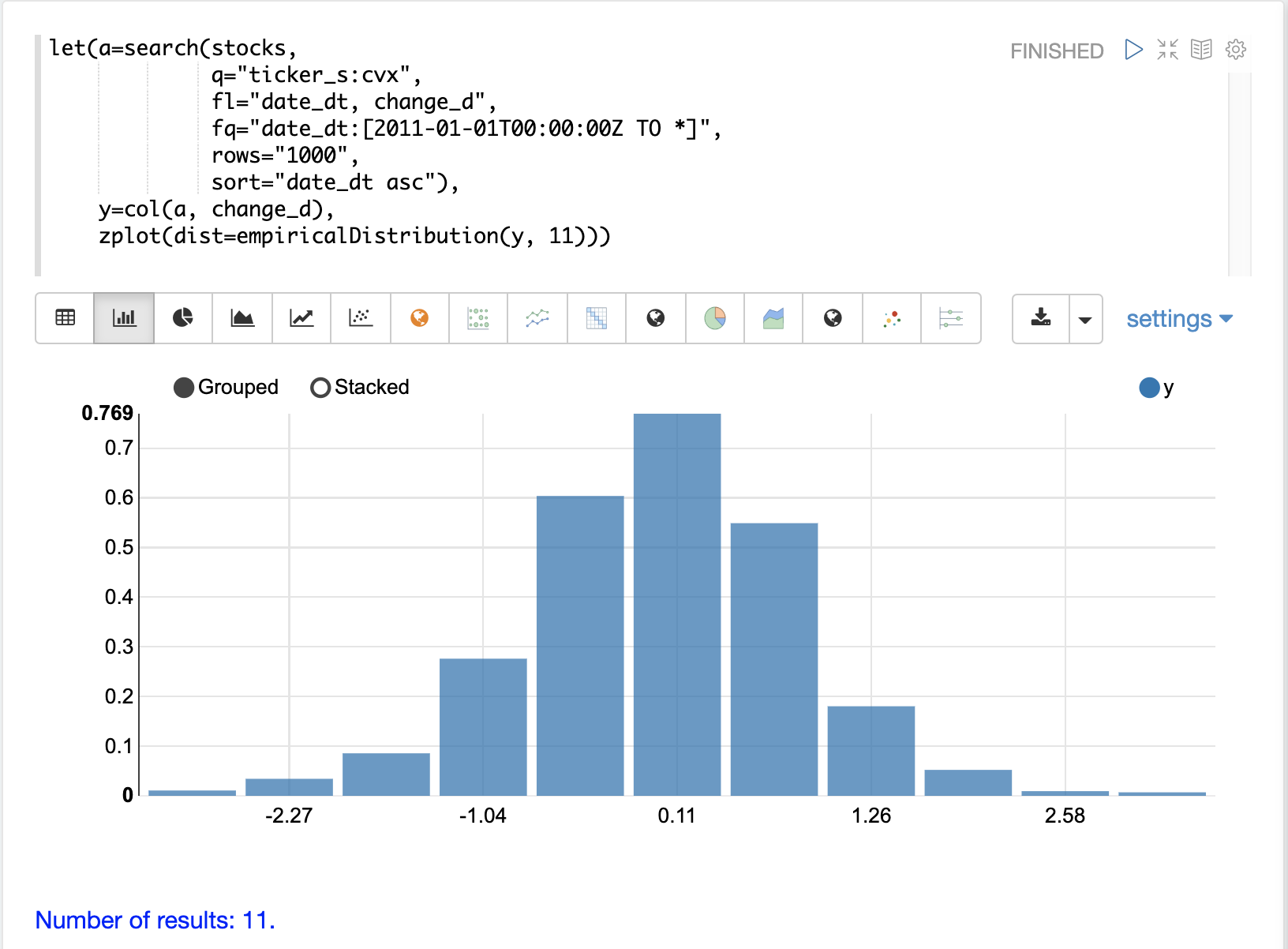
拟合分布
ks 检验可用于确定数据向量的分布是否符合参考分布。在下面的示例中,使用 change_d 向量的均值(mean)和标准差(stddev)作为参考分布,对正态分布执行 ks 检验。ks 检验将参考分布与 change_d 向量本身进行比较,以查看它是否符合正态分布。
请注意,在下面的示例中,ks 检验报告的 p 值为 0.16278。通常使用 0.05 或更小的 p 值来否定检验的零假设,即该向量可能来自参考分布。
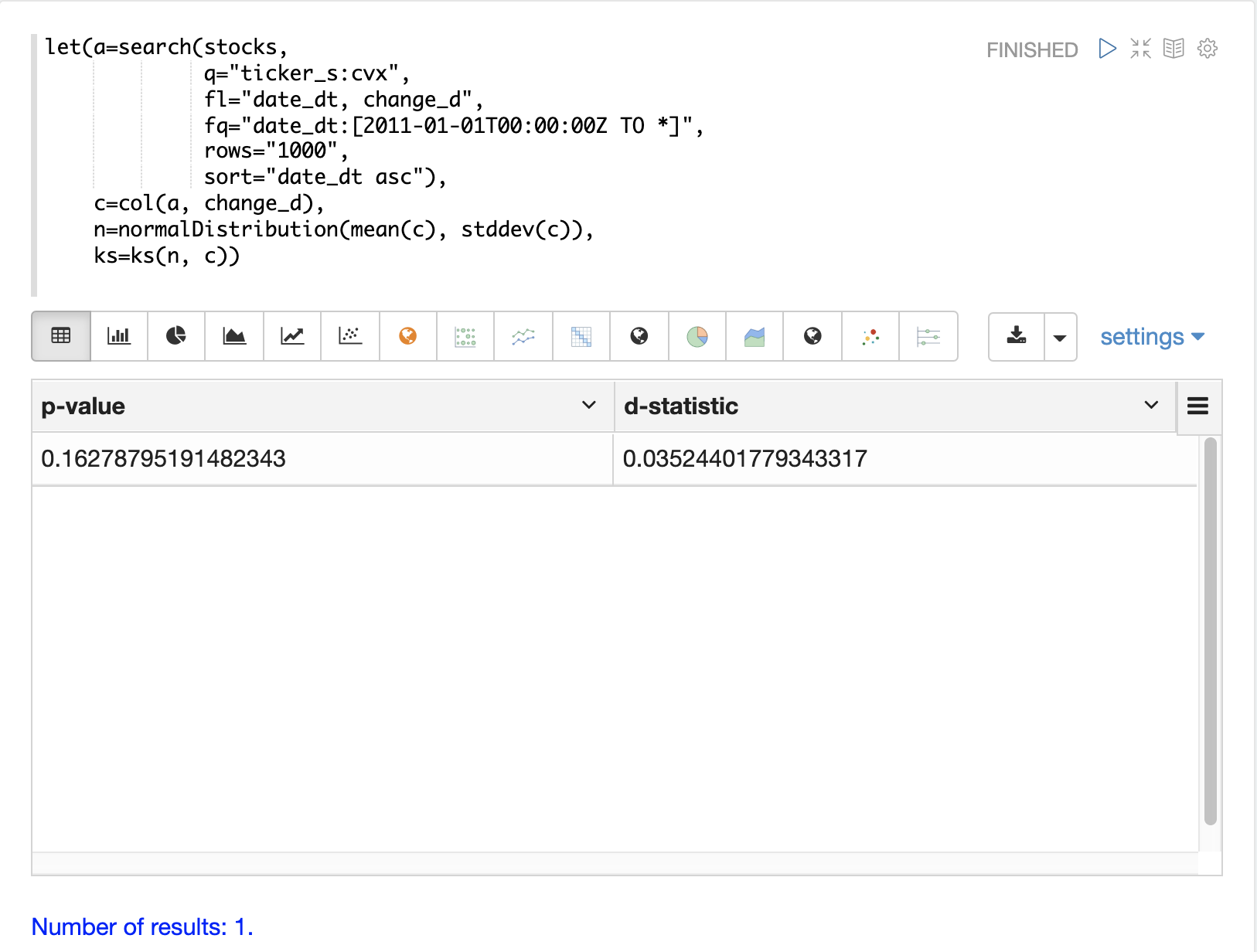
ks 检验往往相当敏感,它证实了看似正态分布的可视化结果。因此,将使用 change_d 向量的均值和标准差的正态分布来表示雪佛龙公司在下面的蒙特卡罗模拟中的每日股票收益。
蒙特卡罗
既然我们已经将分布拟合到每日股票收益数据,我们可以使用 monteCarlo 函数来运行使用该分布的模拟。
monteCarlo 函数运行指定的次数。在每次运行时,它都会设置一系列变量并运行一个返回单个数值的最终函数。monteCarlo 函数将每次运行的结果收集到一个向量中并返回它。最终函数通常有一个或多个变量,这些变量在每次运行时都从概率分布中抽取。sample 函数用于抽取样本。
然后可以将模拟的结果数组视为经验分布,以了解模拟结果的概率。
下面的示例使用 monteCarlo 函数来模拟 100 天股票收益的总回报的分布。
在示例中,从 change_d 向量的均值和标准差创建了一个 normalDistribution。然后,monteCarlo 函数从正态分布中抽取 100 个样本,以表示 100 天的股票收益,并将样本向量设置为变量 d。
然后,add 函数计算 100 天样本的总回报。add 函数的输出由 monteCarlo 函数收集。重复此过程 50000 次,每次运行都从正态分布中抽取一组不同的样本。
模拟的结果设置为变量 s,其中包含来自 50000 次运行的总回报。
然后使用 empiricalDistribution 函数将模拟的输出可视化为 50 个箱子的直方图。该分布可视化了股票代码为 CVX 的股票 100 天股票收益的不同总回报的概率。
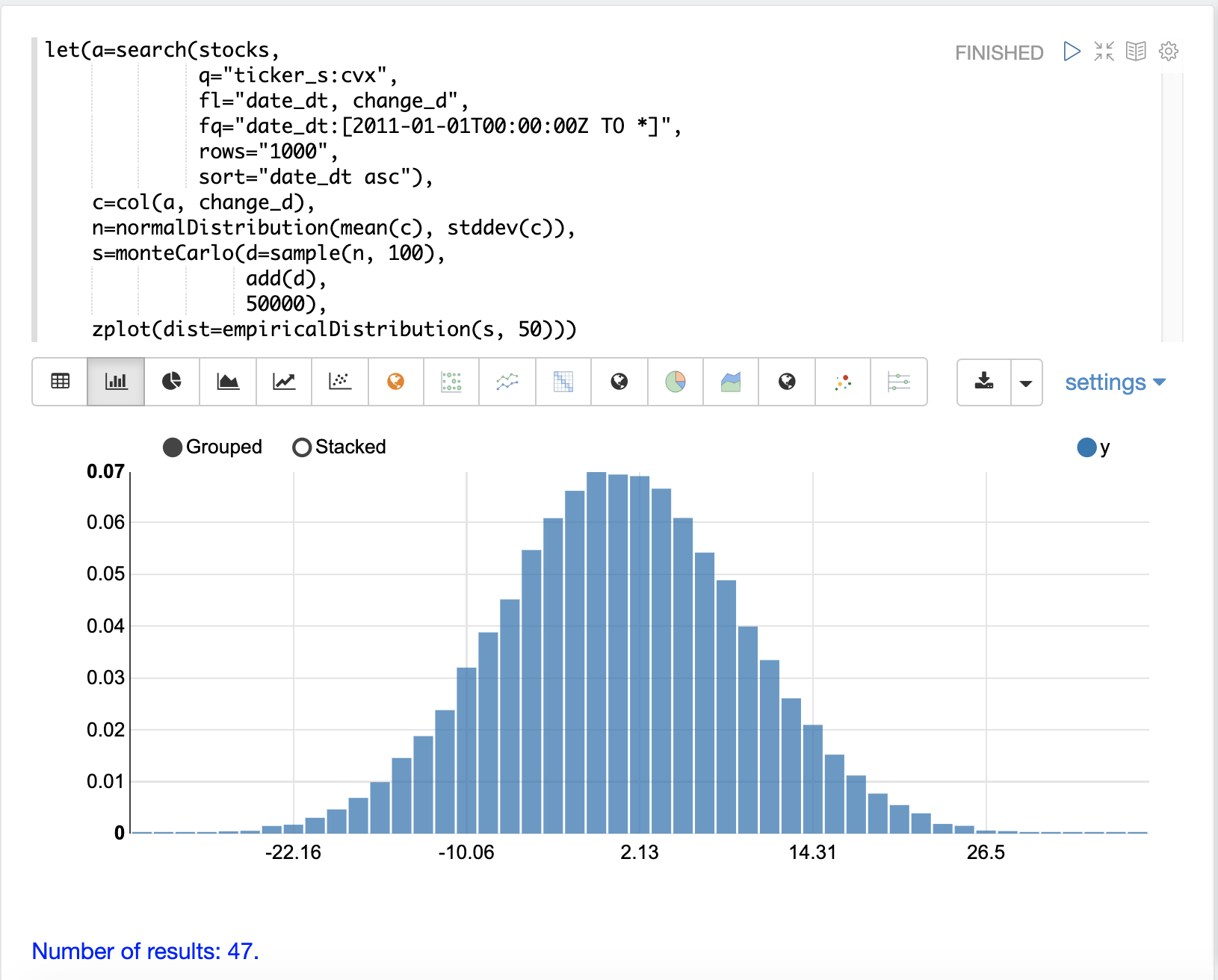
然后可以使用 probability 和 cumulativeProbability 函数来了解有关 empiricalDistribution 的更多信息。例如,probability 函数可用于计算 100 天股票收益的非负回报的概率。
下面的示例使用 probability 函数返回模拟的 empiricalDistribution 中 0 到 40 之间的回报概率。
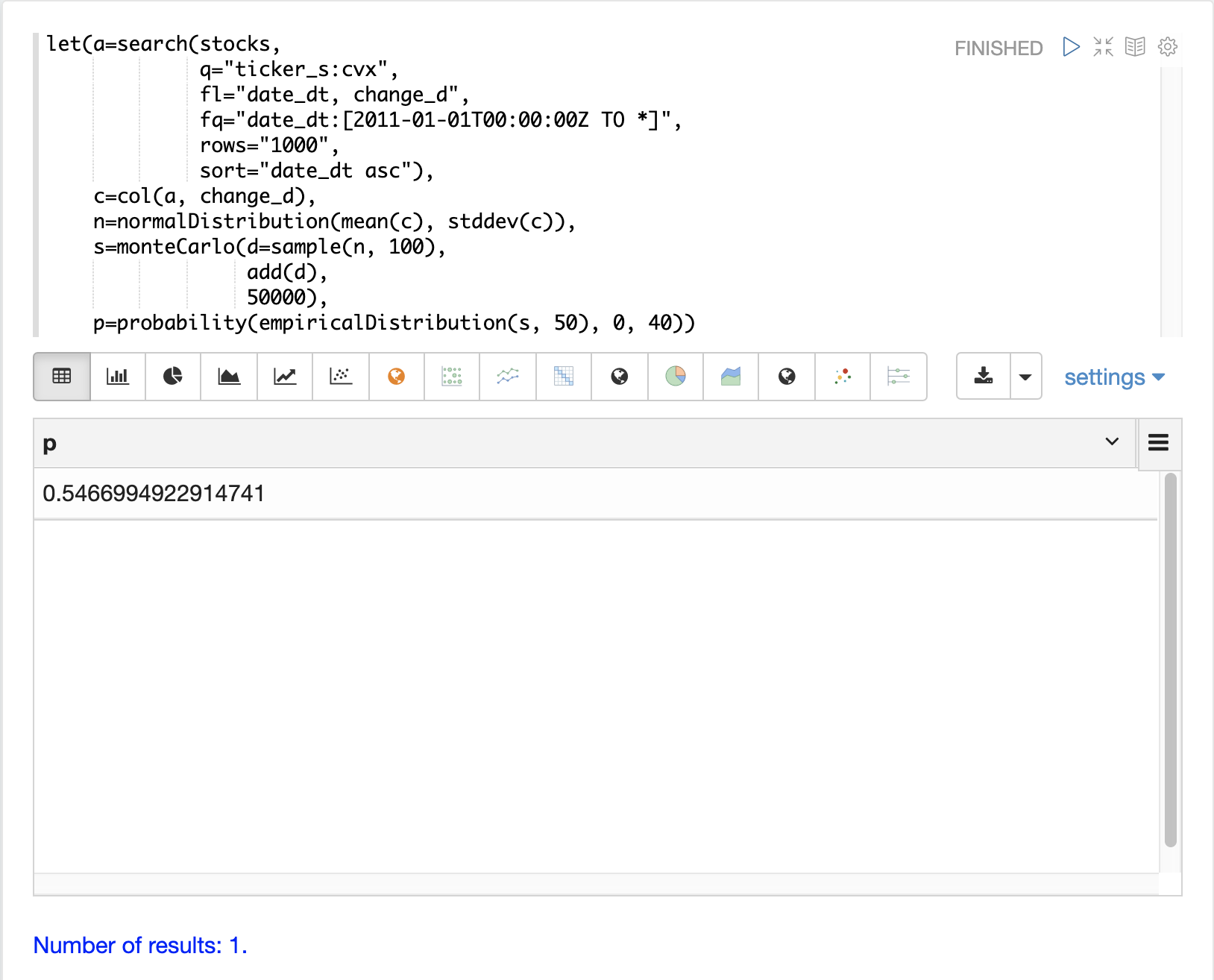
随机游走
monteCarlo 函数还可用于根据每日股票收益的 normalDistribution 模拟每日股票价格的随机游走。随机游走是一个时间序列,其中每个步骤都是通过将随机样本添加到上一步来计算的。这将创建一个时间序列,其中每个值都取决于前一个值,从而模拟股票价格的自相关性。
在下面的示例中,通过在每次蒙特卡罗迭代时将随机样本添加到变量 v 来实现随机游走。变量 v 在迭代之间维护,因此每次迭代都使用 v 的先前值。double 函数是每次迭代运行的最终函数,它只是将 v 的值作为 double 返回。该示例迭代 1000 次,以创建具有 1000 个步骤的随机游走。
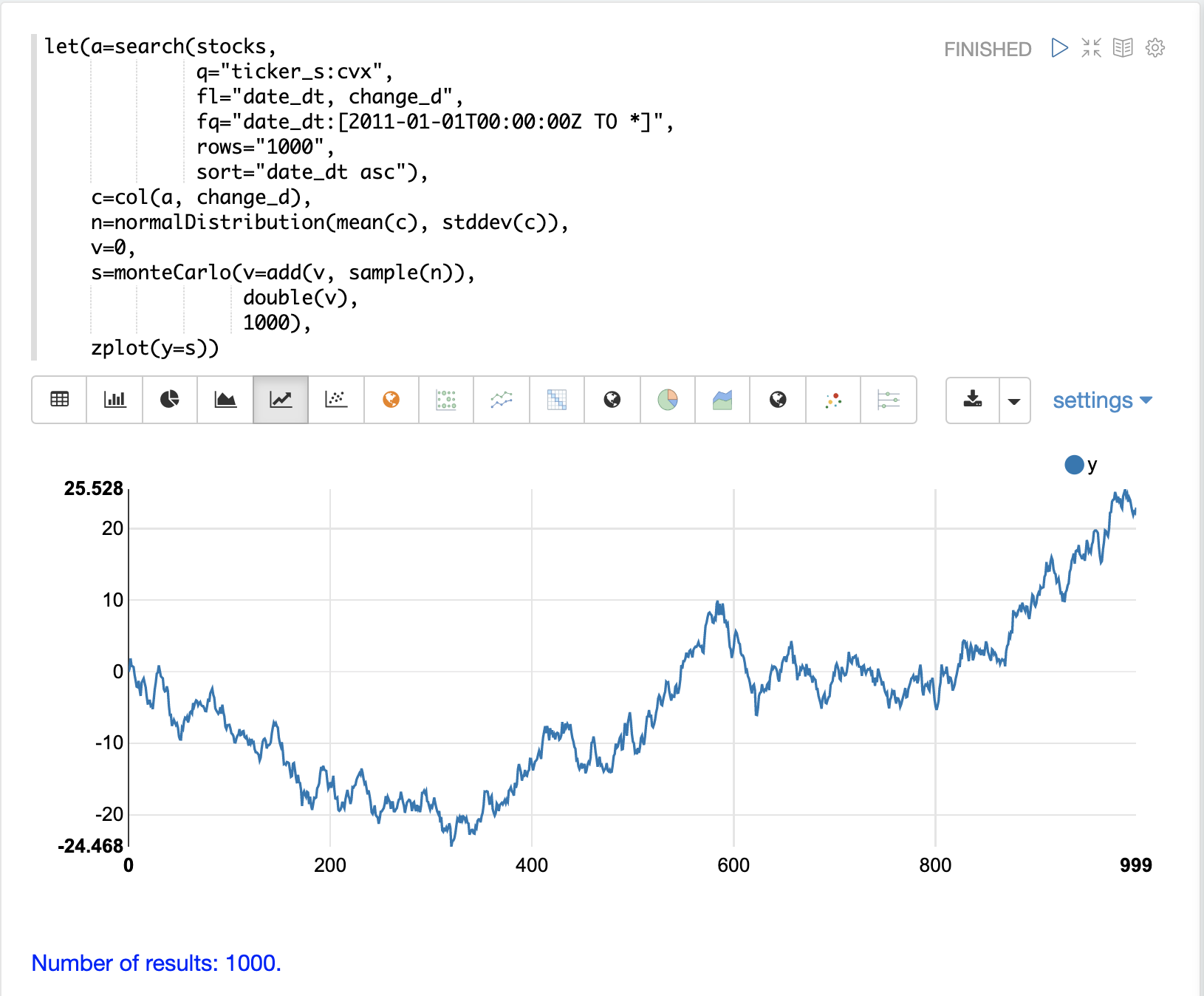
请注意,由于步骤之间的依赖性而导致的每日股票价格的自相关性产生了与股票价格每日随机变化非常不同的图。
多元正态分布
multiVariateNormalDistribution 函数可用于建模和模拟两个或多个正态分布变量。它还将变量之间的相关性纳入模型中,从而可以研究相关性如何影响可能的结果。
在下面的示例中,探讨了两个股票的每日总回报的模拟。使用 ALL 股票代码(Allstate)以及前面示例中的 CVX 股票代码(雪佛龙)。
相关性和协方差
多元模拟显示了相关性对可能结果的影响。在开始实际模拟之前,首先了解 Allstate 和雪佛龙股票收益之间的相关性和协方差会很有帮助。
下面的示例运行两个搜索,以检索所有 Allstate 和雪佛龙的每日股票收益。将两个回报的 change_d 向量读入变量(all 和 cvx),并使用 corr 函数计算两个向量的皮尔逊相关性。
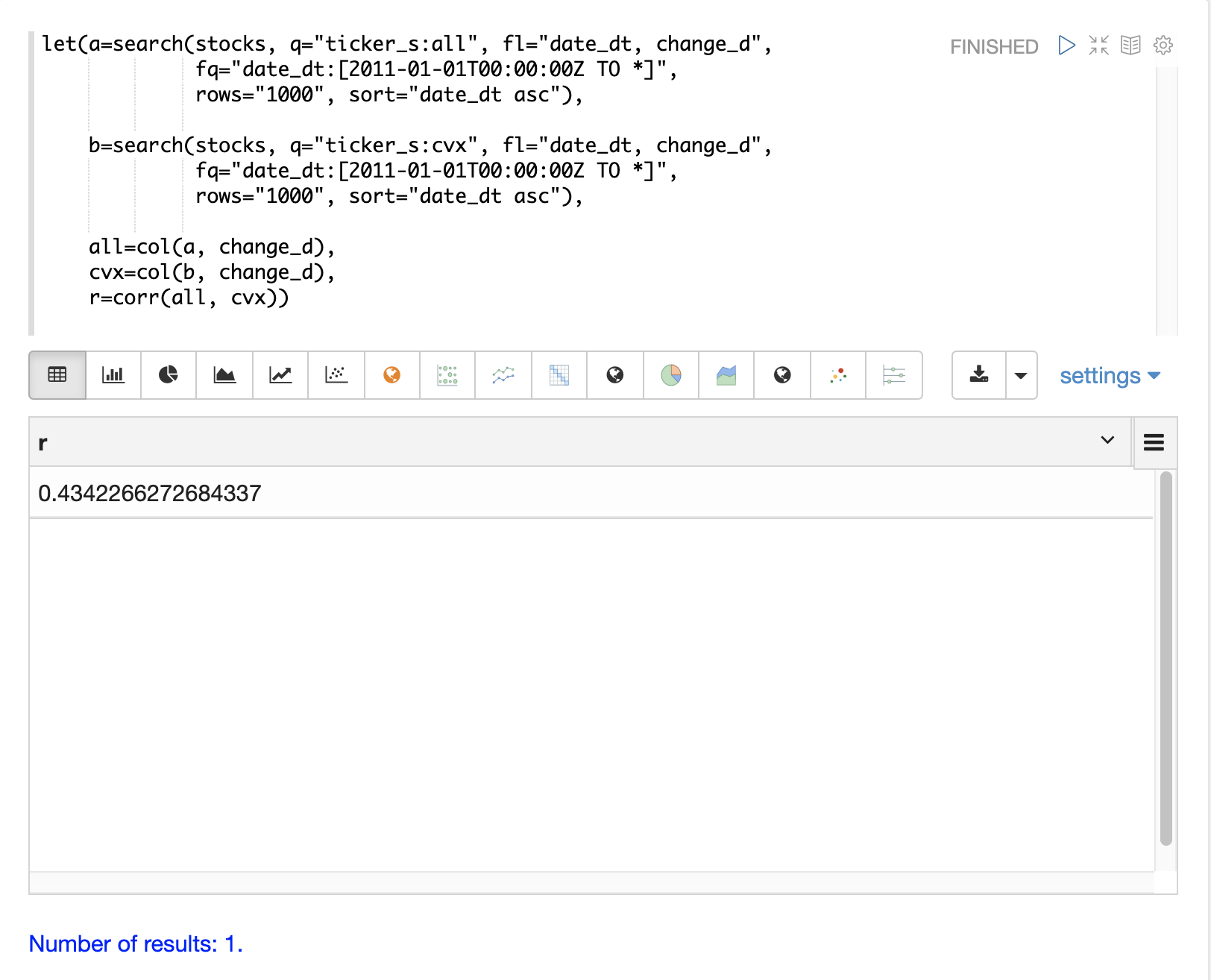
协方差是未缩放的相关性度量。协方差是多元模拟使用的度量,因此计算两个股票收益的协方差也很有用。下面的示例计算协方差。
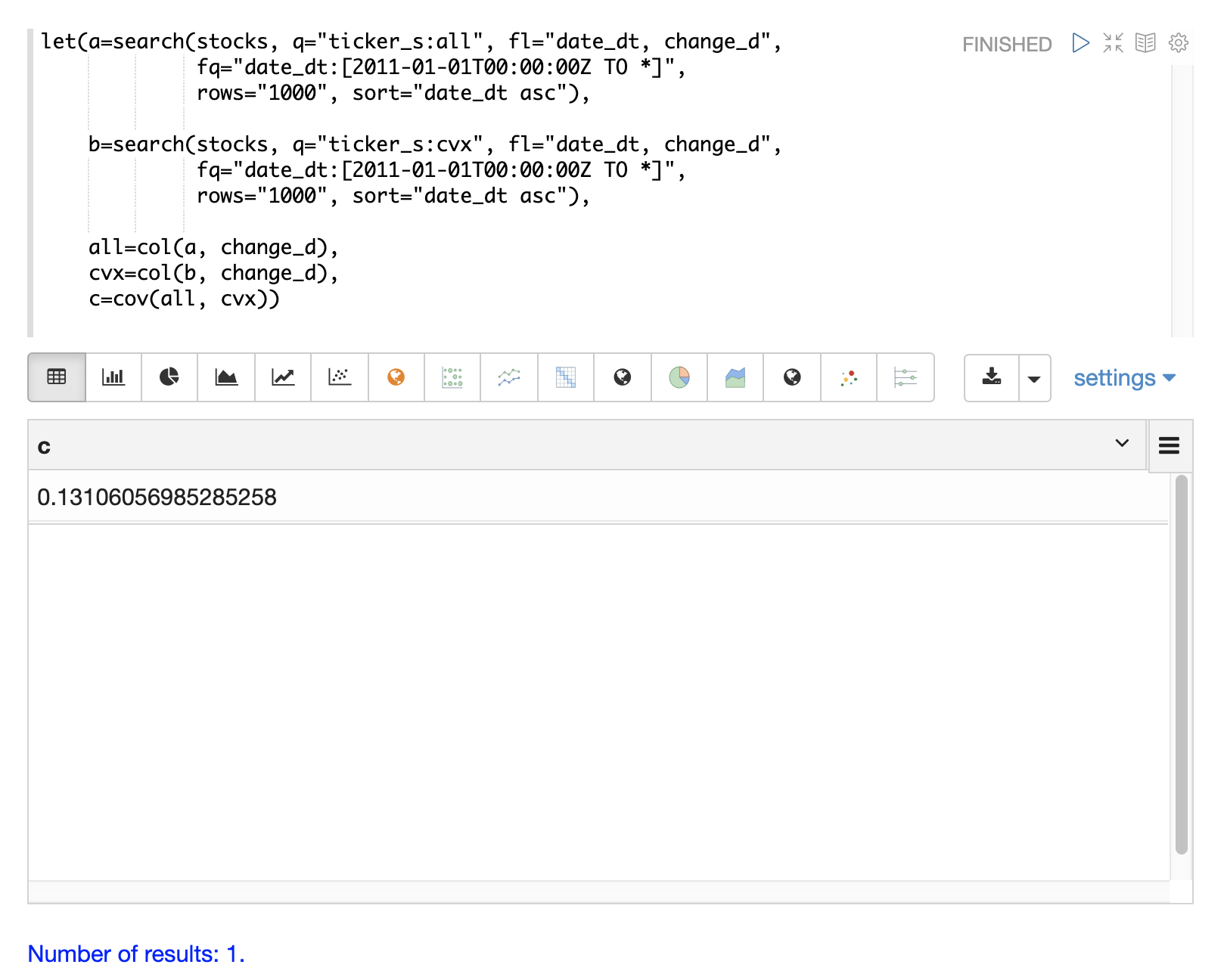
协方差矩阵
multiVariateNormalDistribution 实际上需要的是协方差矩阵,因为它既包含两个股票收益向量的方差,也包含两个向量之间的协方差。cov 函数将计算矩阵列的协方差矩阵。
下面的示例演示如何通过将 all 和 cvx 向量作为行添加到矩阵来计算协方差矩阵。然后使用 transpose 函数转置该矩阵,以便 all 向量是第一列,而 cvx 向量是第二列。
然后,cov 函数计算矩阵列的协方差矩阵并返回结果。
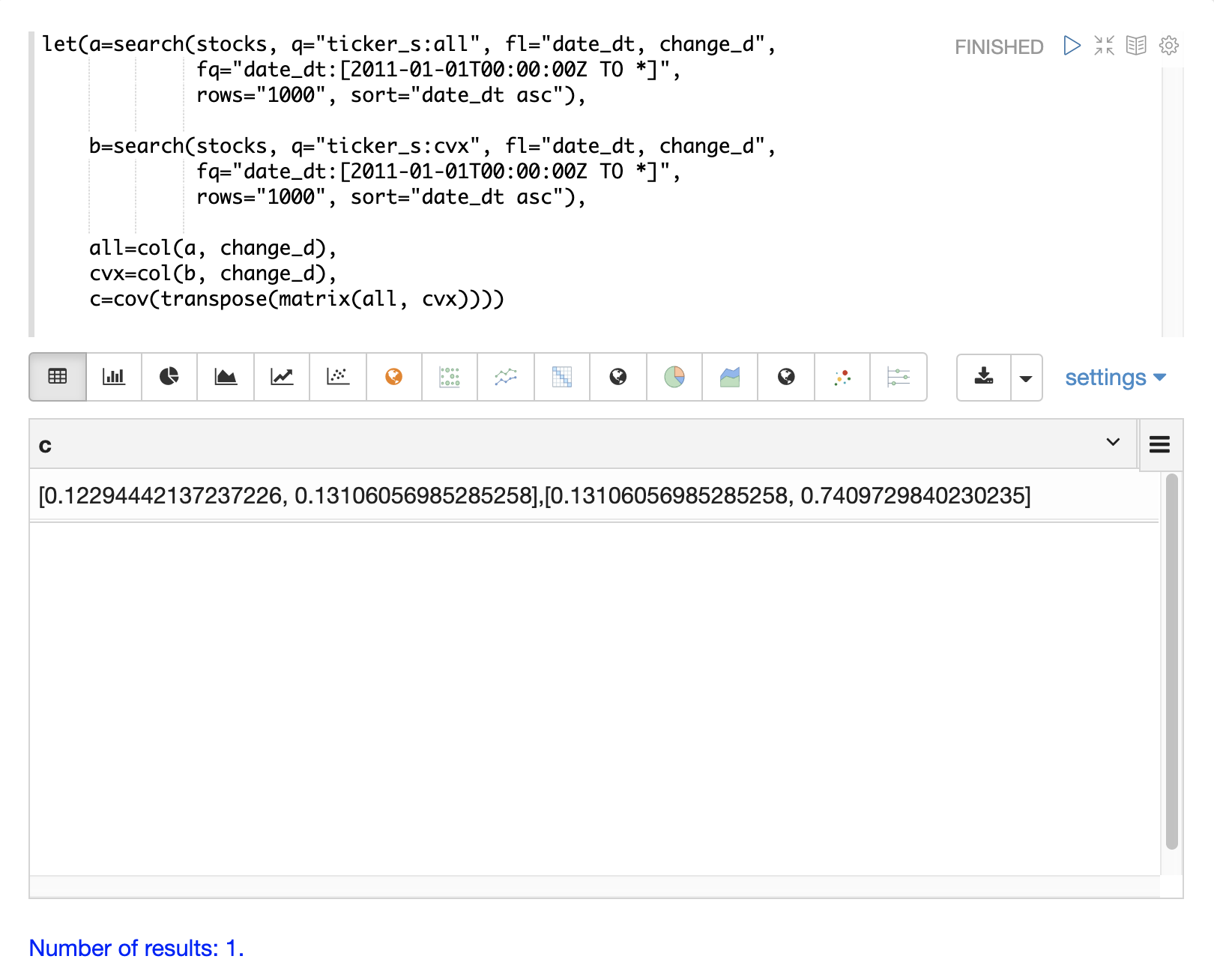
协方差矩阵是一个方阵,其中包含每个向量的方差以及向量之间的协方差,如下所示
all cvx
all [0.12294442137237226, 0.13106056985285258],
cvx [0.13106056985285258, 0.7409729840230235]多元模拟
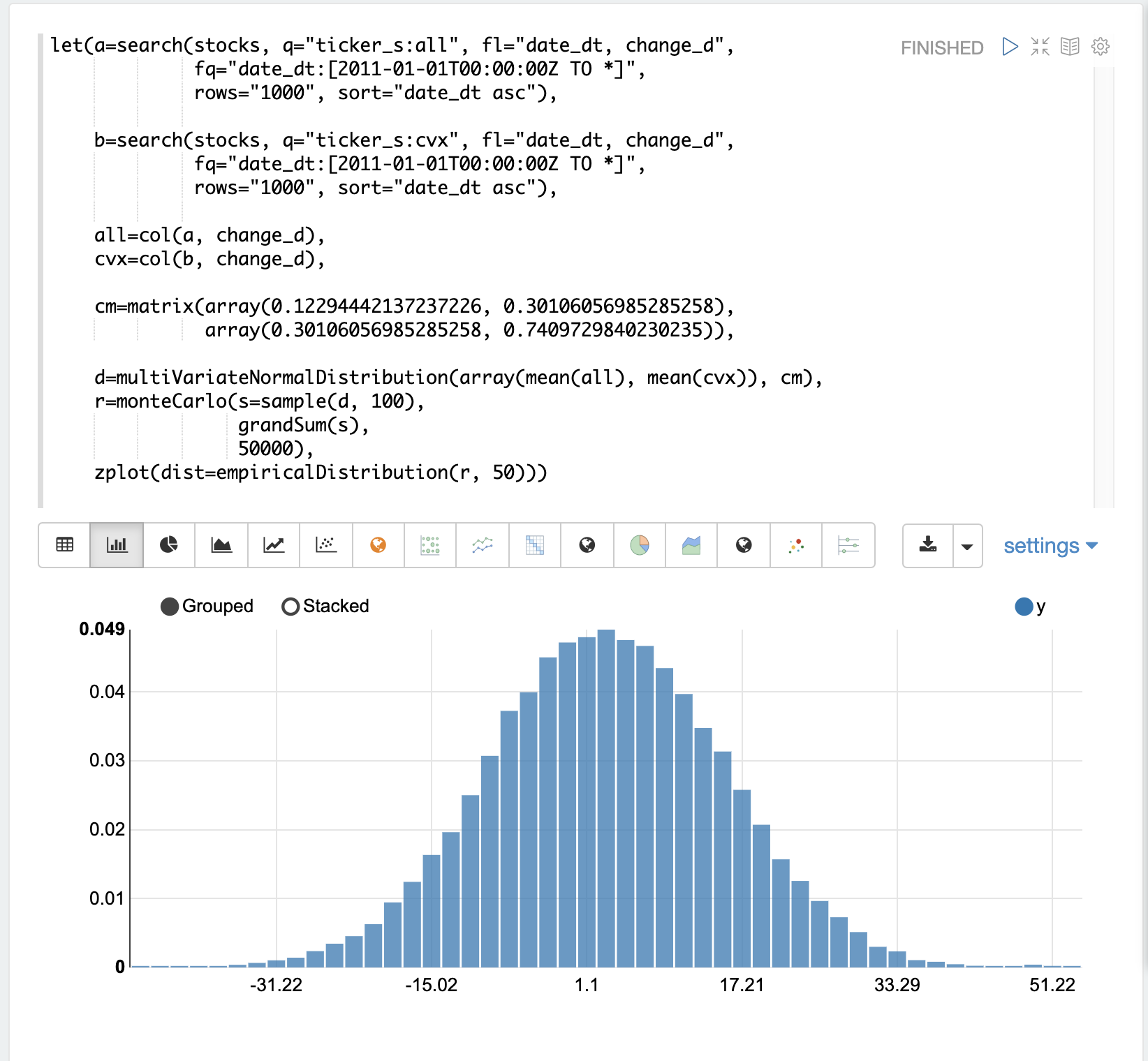
下面的示例演示了使用 multiVariateNormalDistribution 的两个股票代码的蒙特卡罗模拟。
在该示例中,检索并读取包含两个股票代码(all(Allstate)和 cvx(雪佛龙))的 change_d 字段的结果集到向量中。
然后从两个向量创建一个矩阵并进行转置,以便该矩阵包含两列,一列包含 all 向量,另一列包含 cvx 向量。
然后,使用两个参数创建 multiVariateNormalDistribution。第一个参数是 mean 值的数组。在这种情况下,是 all 向量和 cvx 向量的均值。第二个参数是协方差矩阵,它是从两个向量的 2 列矩阵创建的。
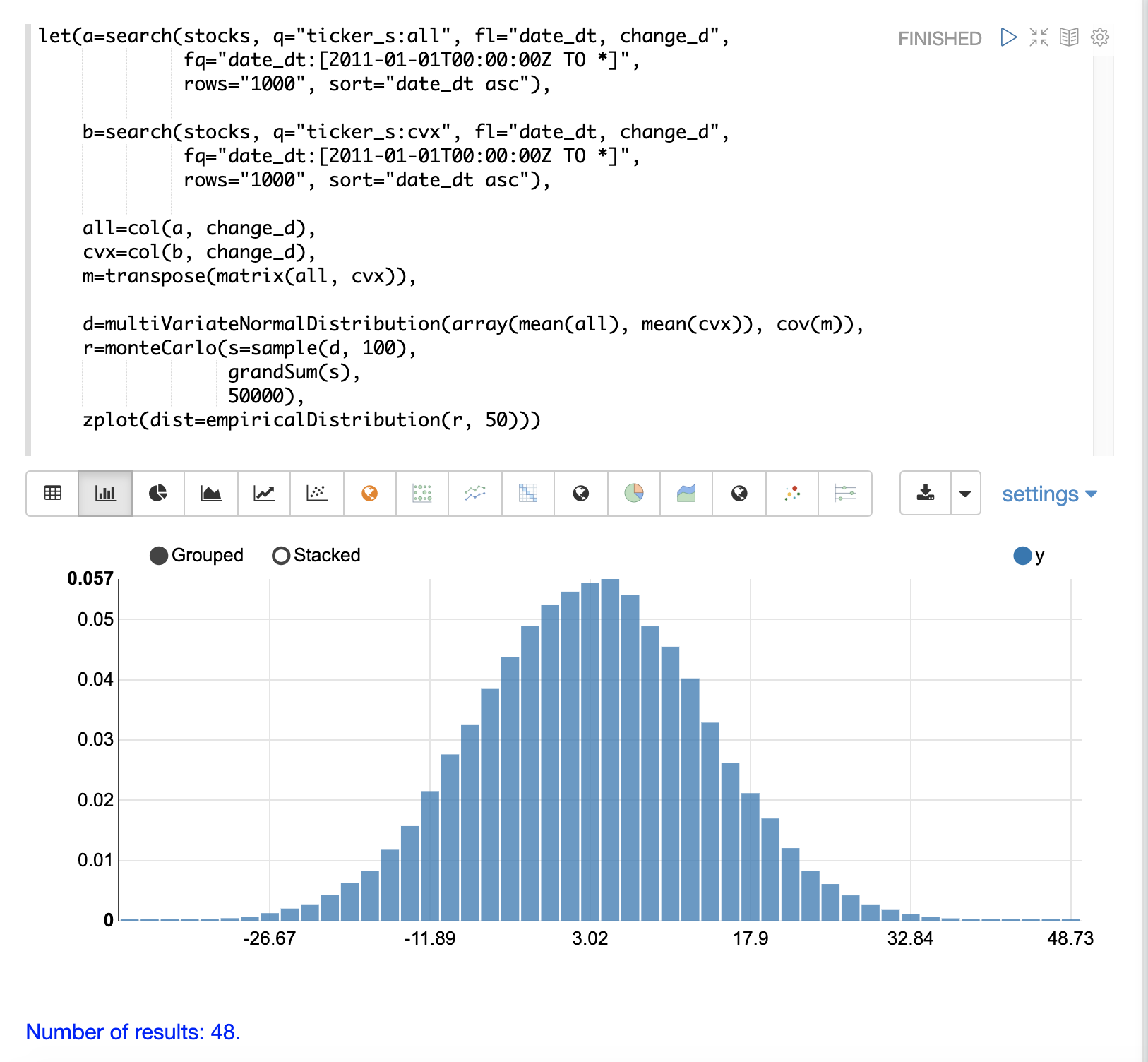
然后,monteCarlo 函数通过在每次迭代时从 multiVariateNormalDistribution 中抽取 100 个样本来执行模拟。每个样本集都是一个包含 100 行和 2 列的矩阵,其中包含来自 all 和 cvx 分布的股票收益样本。列的分布将匹配用于创建 multiVariateNormalDistribution 的正态分布。样本列的协方差将匹配协方差矩阵。
在每次迭代中,使用 grandSum 函数对样本矩阵的所有值求和,以获得两只股票的总股票收益。
模拟的输出是一个向量,其处理方式与单只股票代码模拟完全相同,可以将其视为经验分布。在此示例中,它被绘制为 50 个箱子的直方图,其中可视化了股票代码为 all 和 cvx 的股票 100 天股票收益的不同总回报的概率。