插值、导数和积分
本节探讨用于插值和数值微积分的相互关联的数学表达式。
插值
插值用于在一组已知的控制点之间构建新的数据点。预测新数据点的能力允许沿着由控制点定义的曲线进行采样。
下面描述的插值函数都返回一个插值函数,该函数可以传递给其他使用采样能力的函数。
如果直接返回,插值函数将返回一个数组,其中包含每个控制点的预测值。这在loess插值的情况下很有用,它首先平滑控制点,然后插值平滑后的点。所有其他插值函数仅返回原始控制点,因为插值预测一条通过原始控制点的曲线。
有不同的插值算法,它们会在曲线上产生不同的预测。数学表达式库当前支持以下插值函数
-
lerp: 线性插值预测通过每个控制点的点,并在控制点之间形成直线。 -
spline: 样条插值预测通过每个控制点的点,并在控制点之间形成平滑曲线。 -
akima: Akima 样条插值与样条插值类似,但对异常值稳定。 -
loess: Loess 插值首先执行非线性局部回归以平滑原始控制点。然后使用样条插值来插值平滑后的控制点。
沿曲线采样
理解插值的一种方法是可视化沿曲线采样的含义。下面的示例通过采样特定 x 轴范围之间的曲线来放大曲线的特定区域。
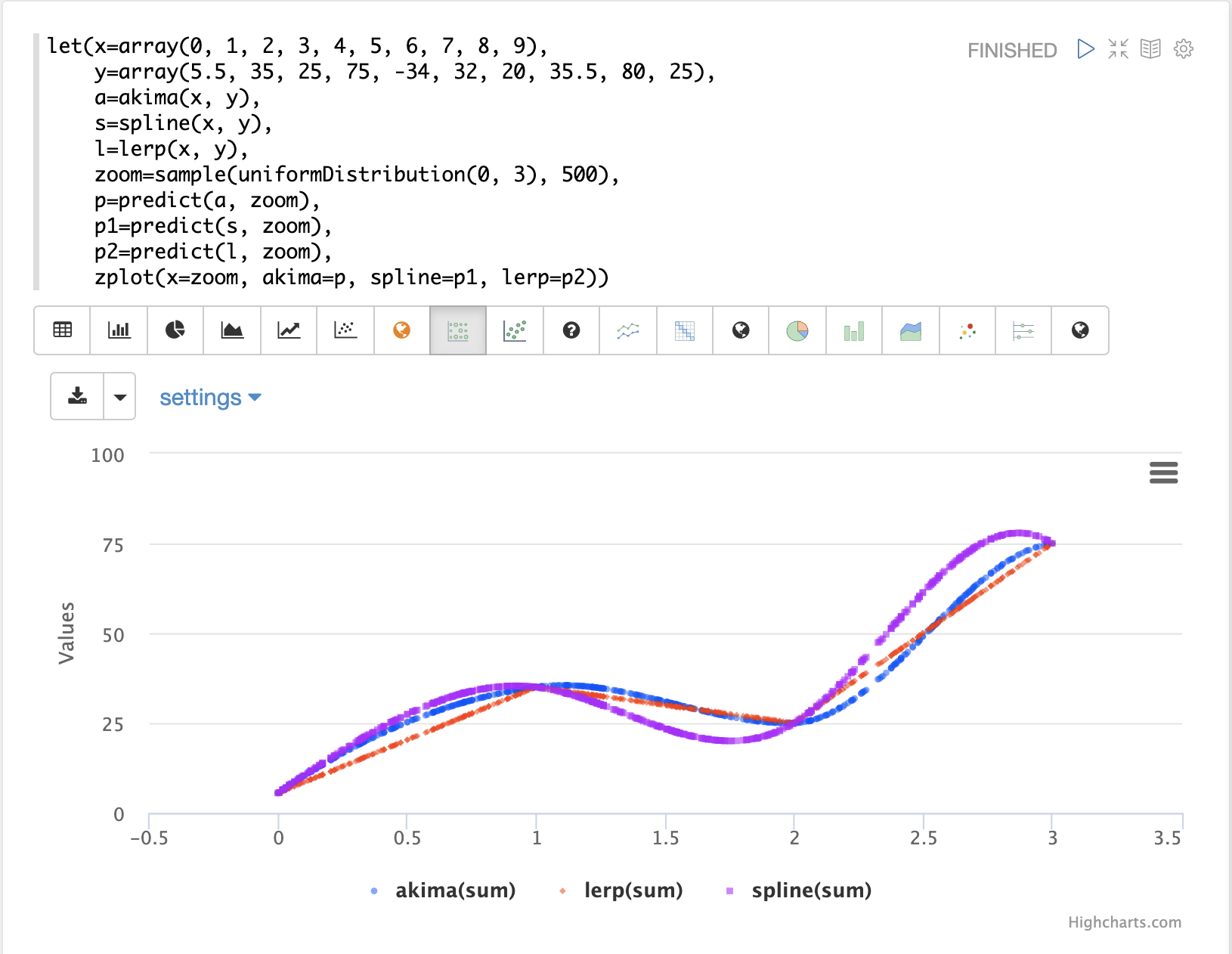
上面的可视化首先创建两个带有 x 轴和 y 轴点的数组。请注意,x 轴范围为 0 到 9。然后将 akima、spline 和 lerp 函数应用于向量以创建三个插值函数。
然后从 0 到 3 之间的均匀分布中抽取 500 个随机样本。这些是新的放大后的 x 轴点,范围在 0 到 3 之间。请注意,我们正在采样曲线的特定区域。
然后使用 predict 函数来预测所有三个插值函数的采样 x 轴的 y 轴点。最后,将所有三个预测向量与采样 x 轴点一起绘制。
红线是 lerp 插值,蓝线是 akima 插值,紫线是 spline 插值。您可以看到它们在控制点之间产生不同的曲线。
平滑插值
loess 函数是一种平滑插值器,这意味着它不会导出一个通过原始控制点的函数。相反,loess 函数返回一个平滑原始控制点的函数。
一种称为局部回归的技术用于计算平滑曲线。可以调整局部回归的邻域大小以控制新曲线与原始控制点的一致程度。
loess 函数接收 x 轴和 y 轴数据,并对数据拟合一条平滑曲线。如果只提供一个数组,则将其视为 y 轴,并为 x 轴生成一个序列。
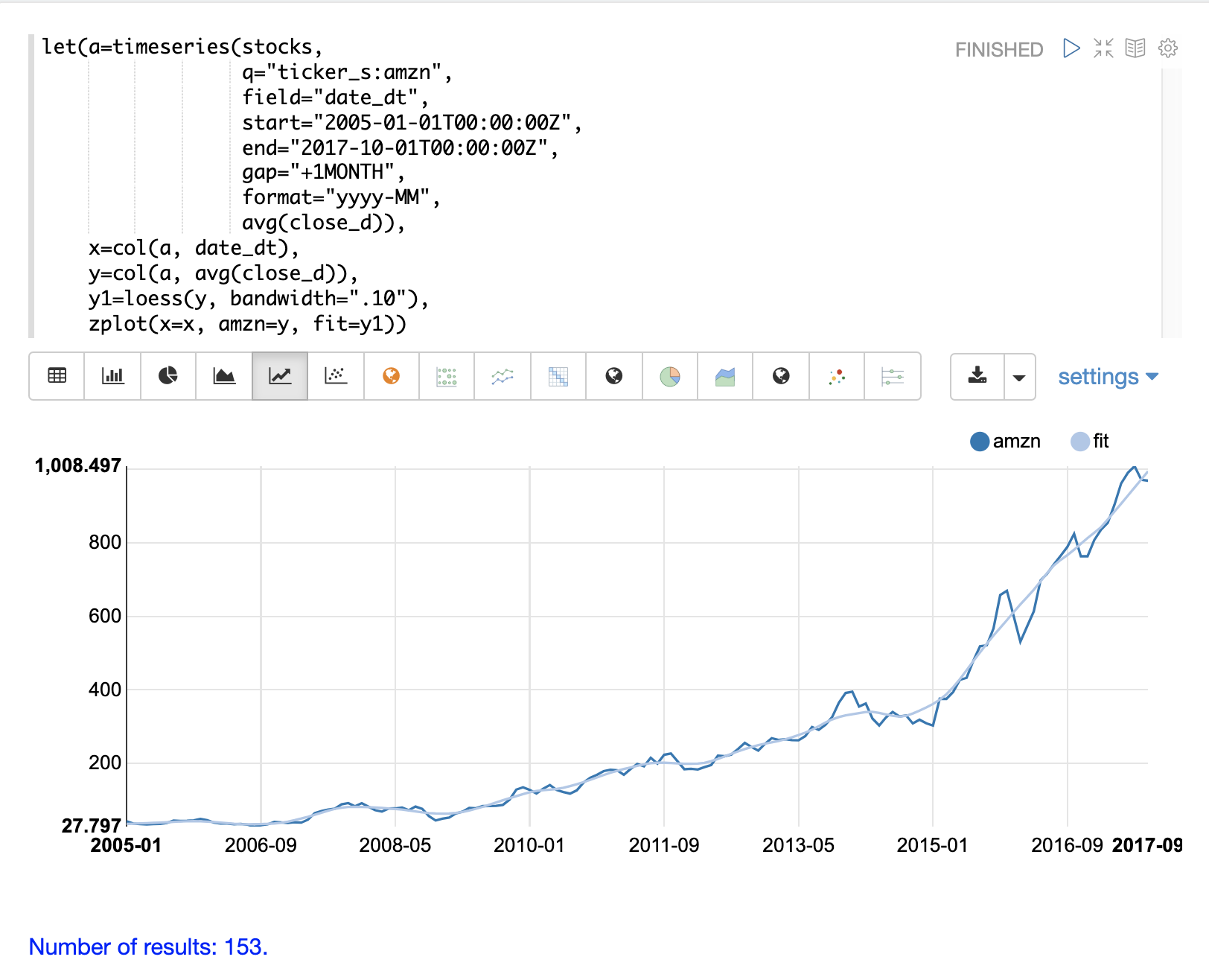
下面的示例展示了如何使用 loess 函数来建模月度时间序列。在这个示例中,timeseries 函数用于生成股票代码为 AMZN 的月度平均收盘价时间序列。然后,时间序列中的 date_dt 和 avg(close_d) 字段被向量化并存储在变量 x 和 y 中。接着,将 loess 函数应用于包含平均收盘价的 y 向量。bandwidth 命名参数指定用于计算局部回归的数据集百分比。loess 函数返回平滑数据点的拟合模型。
然后,使用 zplot 函数绘制 x、y 和 y1 变量。
导数
函数的导数衡量 y 值相对于 x 值变化率的变化率。
derivative 函数可以计算上述任何插值函数的导数。每个插值函数都会产生不同的导数,这些导数与该函数的特性相匹配。
一阶导数(速度)
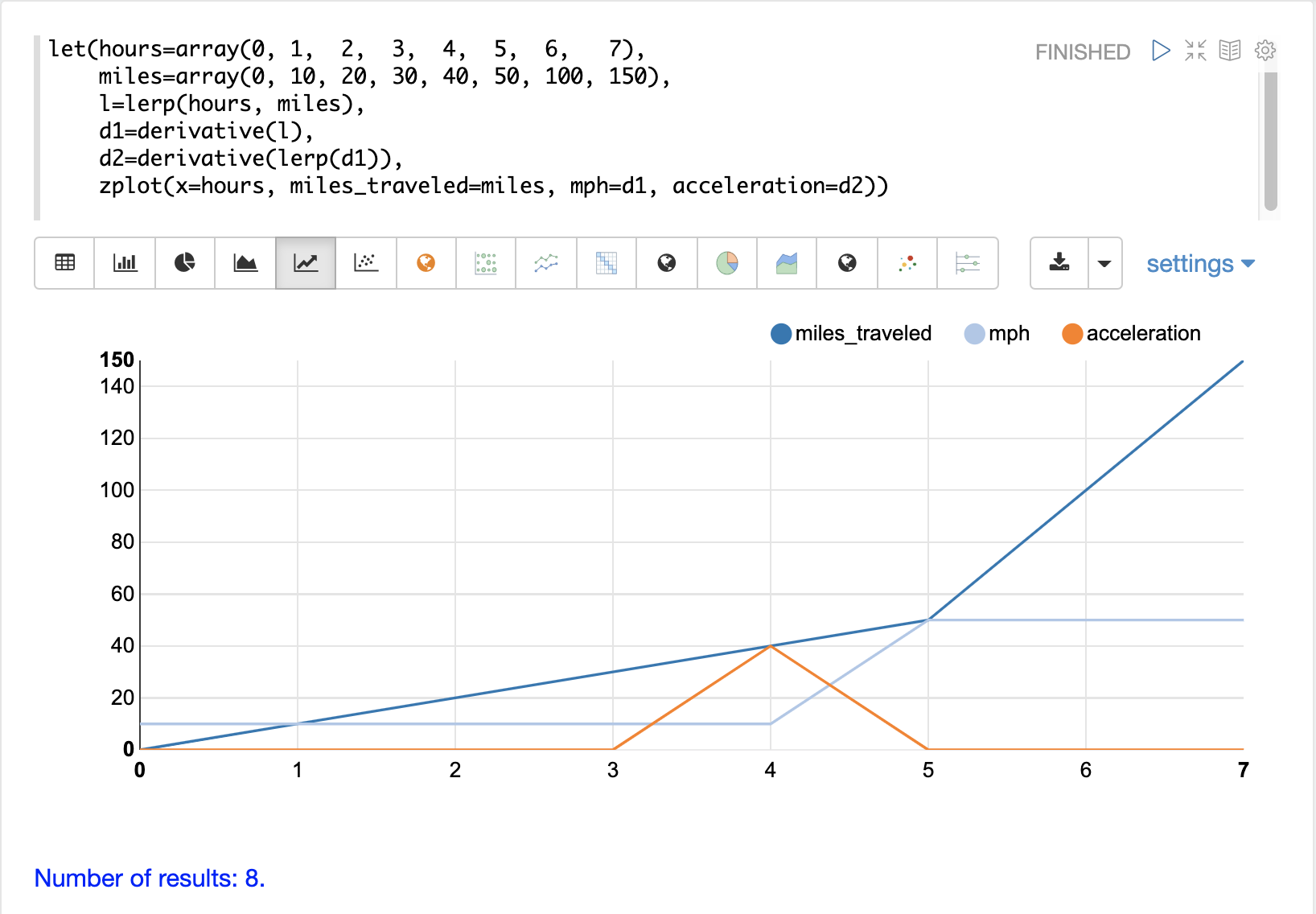
一个简单的例子展示了如何使用 derivative 函数计算变化率或速度。
在这个例子中,创建了两个向量,一个代表小时数,另一个代表行驶的里程数。然后,使用 lerp 函数创建 hours 和 miles 向量的线性插值。接着,将 derivative 函数应用于线性插值。然后使用 zplot 在 x 轴上绘制 hours,在 y 轴上绘制 miles,并在每个 x 轴点绘制 derivative 作为 mph。
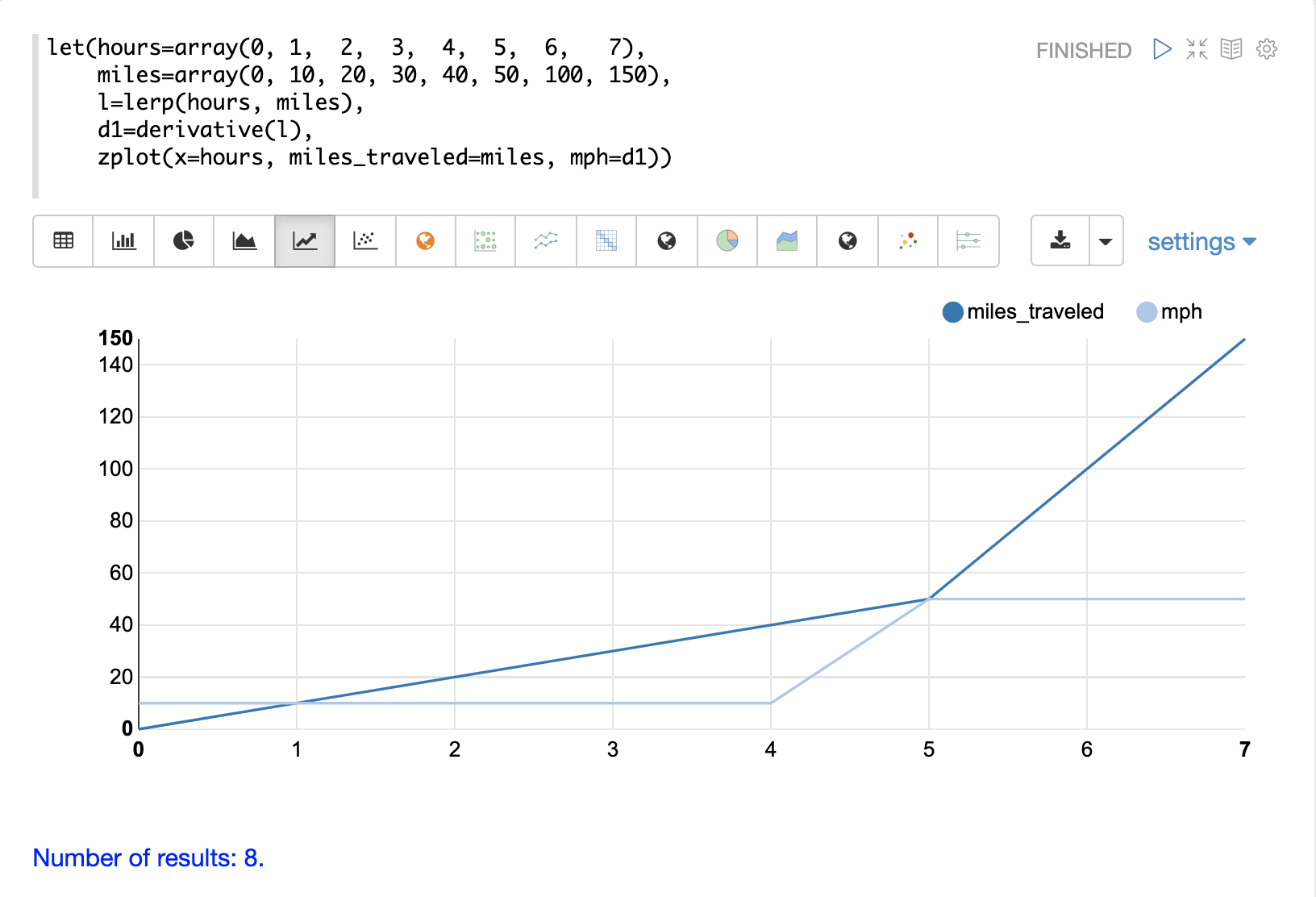
请注意,miles_traveled 线在第 5 个小时之前斜率为 10,之后变为 50。mph 线,即导数,可视化了 miles_traveled 线的速度。
另请注意,导数是沿着直线计算的,显示了从一个点到下一个点的立即变化。这是因为线性插值 (lerp) 用作插值函数。如果使用 spline 或 akima 函数,则会产生带有圆曲线的导数。
积分
积分是曲线下面积的度量。integral 函数计算曲线的累积积分或插值曲线特定范围内的积分。与 derivative 函数类似,integral 函数在插值函数上运行。
单积分
如果 integral 函数传入一个开始和结束范围,它将计算该特定范围内曲线下的面积。
在下面的示例中,integral 函数计算曲线整个范围(0 到 10)的积分。请注意,integral 函数被传递了插值曲线以及开始和结束范围,并返回该范围的积分。
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integral=integral(curve, 0, 10))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"integral": 45.300912584519914
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}累积积分图
如果 integral 函数被传递了一条单一插值曲线,它会返回该曲线累积积分的向量。累积积分向量包含每个 x 轴点的累积积分计算。累积积分是通过取每个 x 轴点和第一个 x 轴点之间的范围的积分来计算的。在上面的例子中,这意味着计算一个积分向量,如下所示
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integrals=array(0, integral(curve, 0, 1), integral(curve, 0, 2), integral(curve, 0, 3), ...)累积积分图可视化了每个 x 轴点下曲线的累积面积。
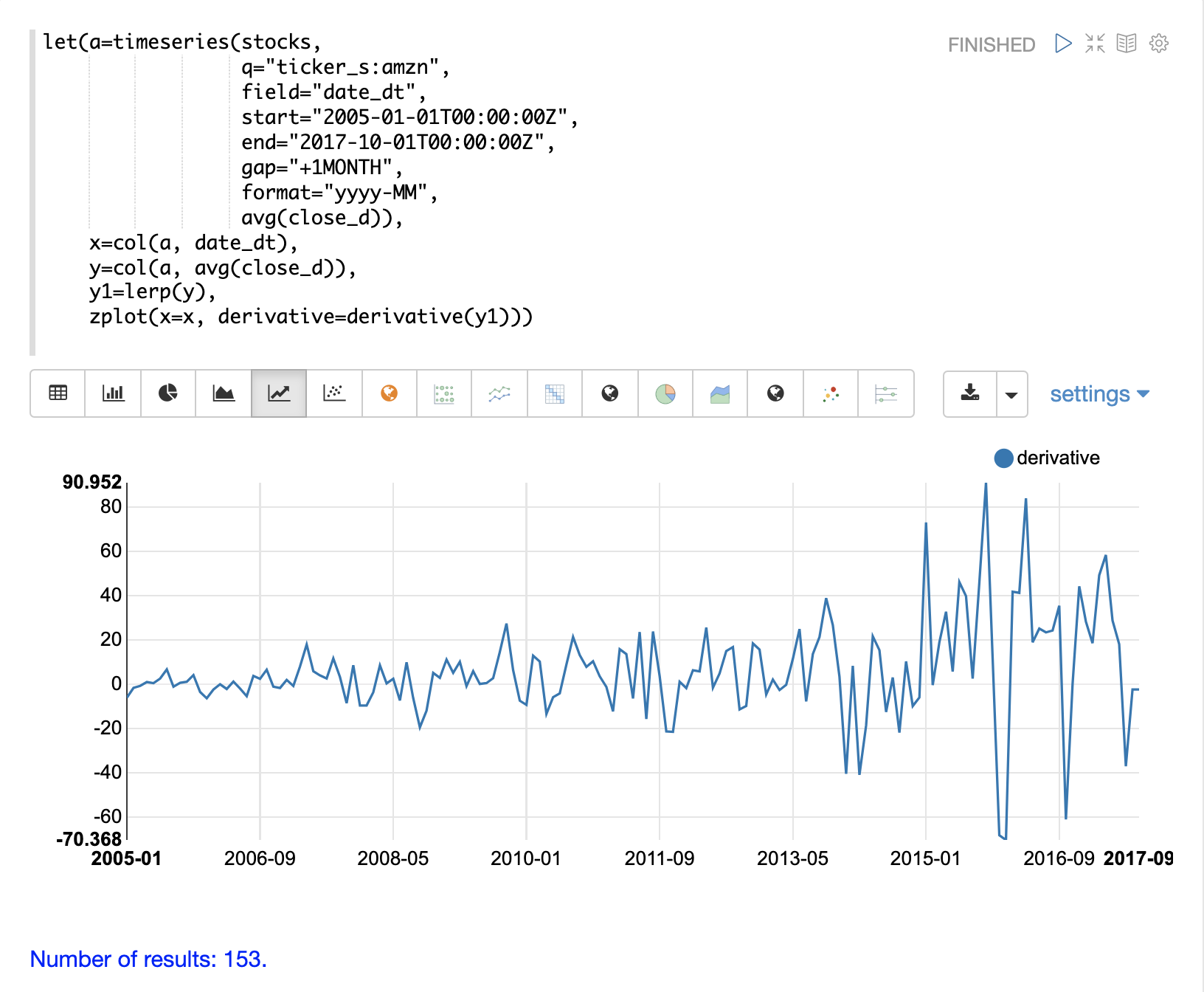
下面的示例显示了由 timeseries 函数生成的时间序列的累积积分图。在这个示例中,生成股票代码为 amzn 的平均收盘价的月度时间序列。avg(close) 列被向量化并使用 spline 进行插值。
然后,使用 zplot 函数绘制时间序列的累积积分。
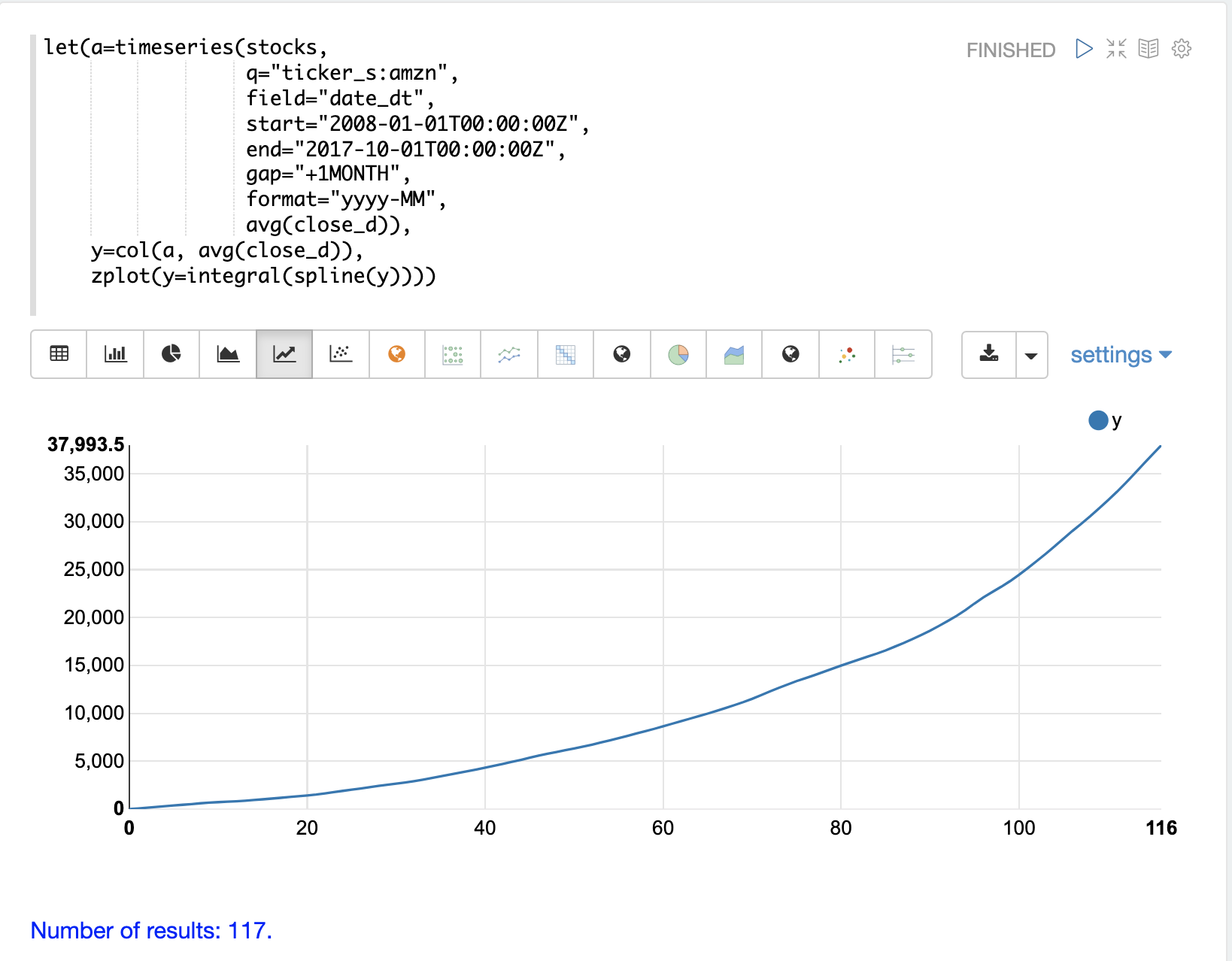
上面的图表可视化了随着 AMZN 股票价格随时间变化,曲线下的面积。因为这个图是累积的,所以如果股票价格时间序列随着时间的推移保持不变,那么它将具有正的线性斜率。价格上涨的股票将具有凹形,而价格下跌的股票将具有凸形。
在这个特定的例子中,积分图随着时间的推移变得更加凹,显示出股票价格的加速上涨。
双三次样条
bicubicSpline 函数可用于在数据网格中的任何位置插值和预测值。
一个简单的例子将使这一点更加清楚
let(years=array(1998, 2000, 2002, 2004, 2006),
floors=array(1, 5, 9, 13, 17, 19),
prices = matrix(array(300000, 320000, 330000, 350000, 360000, 370000),
array(320000, 330000, 340000, 350000, 365000, 380000),
array(400000, 410000, 415000, 425000, 430000, 440000),
array(410000, 420000, 425000, 435000, 445000, 450000),
array(420000, 430000, 435000, 445000, 450000, 470000)),
bspline=bicubicSpline(years, floors, prices),
prediction=predict(bspline, 2003, 8))在这个示例中,使用双三次样条来插值房地产数据矩阵。矩阵的每一行代表特定的年份。矩阵的每一列代表建筑物的楼层。网格中的数字是每个年份和楼层的公寓平均售价。例如,在 2002 年,9 楼的平均售价为 415000(第 3 行,第 3 列)。
然后使用 bicubicSpline 函数对网格进行插值,并使用 predict 函数预测 2003 年 8 楼的值。请注意,该矩阵不包含 2003 年 8 楼的数据点。bicubicSpline 函数根据矩阵中周围的数据创建该数据点
{
"result-set": {
"docs": [
{
"prediction": 418279.5009328358
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}