线性回归

数学表达式库支持简单和多元线性回归。

简单线性回归

regress 函数用于构建两个随机变量之间的线性回归模型。样本观测值由两个数值数组提供。第一个数值数组是自变量，第二个数组是因变量。

在下面的示例中，random 函数选择 50000 个随机样本，每个样本都包含字段 filesize_d 和 response_d。这两个字段被向量化并存储在变量 x 和 y 中。然后，regress 函数对这两个数值数组执行回归分析。

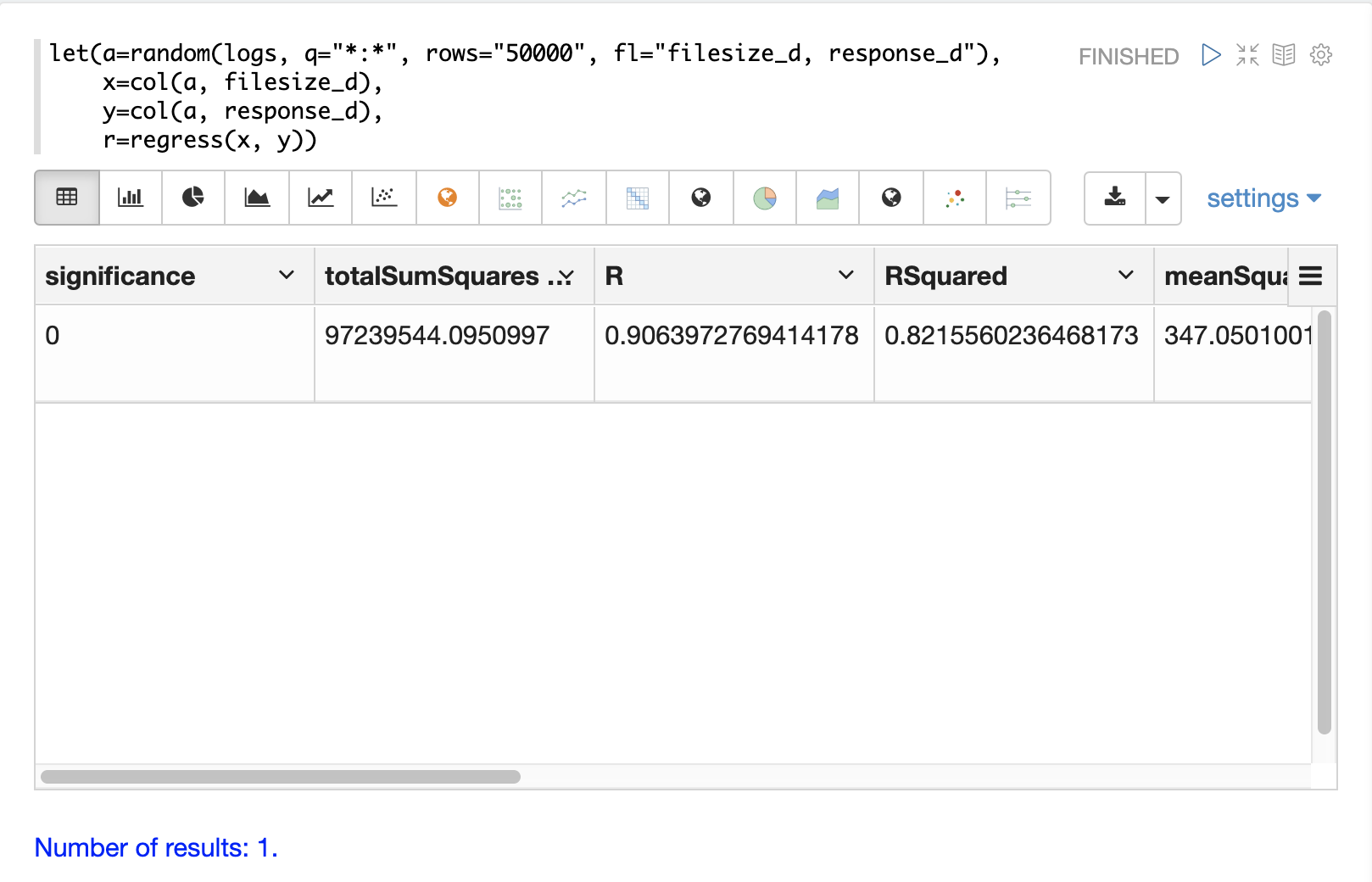
regress 函数返回一个包含回归分析结果的单个元组。

let(a=random(logs, q="*:*", rows="50000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y))

请注意，在此回归分析中，RSquared 的值为 .75。这意味着 filesize_d 的变化解释了 response_d 变量 75% 的变异性

{
  "result-set": {
    "docs": [
      {
        "significance": 0,
        "totalSumSquares": 96595678.64838874,
        "R": 0.9052835767815126,
        "RSquared": 0.8195383543903288,
        "meanSquareError": 348.6502485633668,
        "intercept": 55.64040842391729,
        "slopeConfidenceInterval": 0.0000822026526346821,
        "regressionSumSquares": 79163863.52071753,
        "slope": 0.019984612363694493,
        "interceptStdErr": 1.6792610845256566,
        "N": 50000
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 344
      }
    ]
  }
}

可以使用 Zeppelin-Solr 在表中可视化诊断结果。

diagnostics

预测

predict 函数使用回归模型进行预测。使用上面的示例，可以使用回归模型根据 filesize_d 的值来预测 response_d 的值。

在下面的示例中，predict 函数使用回归分析来预测 filesize_d 值为 40000 时 response_d 的值。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, 40000))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "p": 748.079241022975
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 95
      }
    ]
  }
}

predict 函数还可以预测一系列值。在这种情况下，它返回一个预测数组。

在下面的示例中，predict 函数使用回归分析来预测用于生成模型的 5000 个 filesize_d 样本中的每个样本的值。在这种情况下，会返回 5000 个预测。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, x))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "p": [
          742.2525322514165,
          709.6972488729955,
          687.8382568904871,
          820.2511324266264,
          720.4006432289061,
          761.1578181053039,
          759.1304101159126,
          699.5597256337142,
          742.4738911248204,
          769.0342605881644,
          746.6740473150268
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

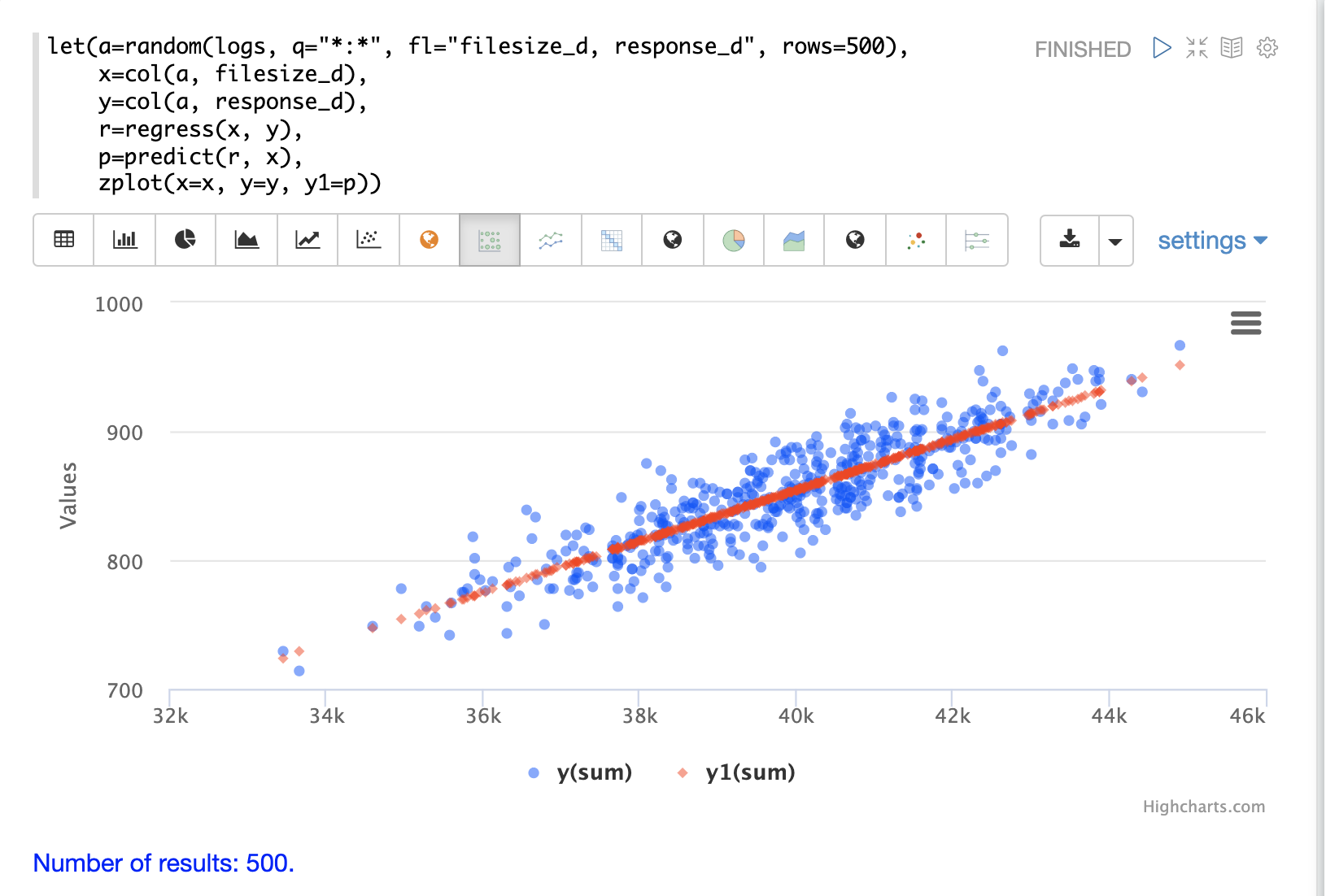
回归图

使用 zplot 和 Zeppelin-Solr 解释器，我们可以在同一散点图中可视化观测值和预测值。在下面的示例中，zplot 在 x 轴上绘制 filesize_d 观测值，在 y 轴上绘制 response_d 观测值，并在 y1 轴上绘制预测值。

linear

残差

观测值和预测值之间的差异称为残差。没有特定的函数来计算残差，但是可以使用向量数学来进行计算。

在下面的示例中，预测值存储在变量 p 中。然后，使用 ebeSubtract 函数从存储在变量 y 中的实际 response_d 值中减去预测值。变量 e 包含残差数组。

let(a=random(logs, q="*:*", rows="500", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, x),
    e=ebeSubtract(y, p))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "e": [
          31.30678554491226,
          -30.292830927953446,
          -30.49508862647258,
          -30.499884780783532,
          -9.696458959319784,
          -30.521563961535094,
          -30.28380938033081,
          -9.890289849359306,
          30.819723560583157,
          -30.213178859683012,
          -30.609943619066826,
          10.527700442607625,
          10.68046928406568
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

残差图

使用 zplot 和 Zeppelin-Solr，我们可以使用残差图可视化残差。下面的示例残差图在 x 轴上绘制预测值，在 y 轴上绘制预测的误差。

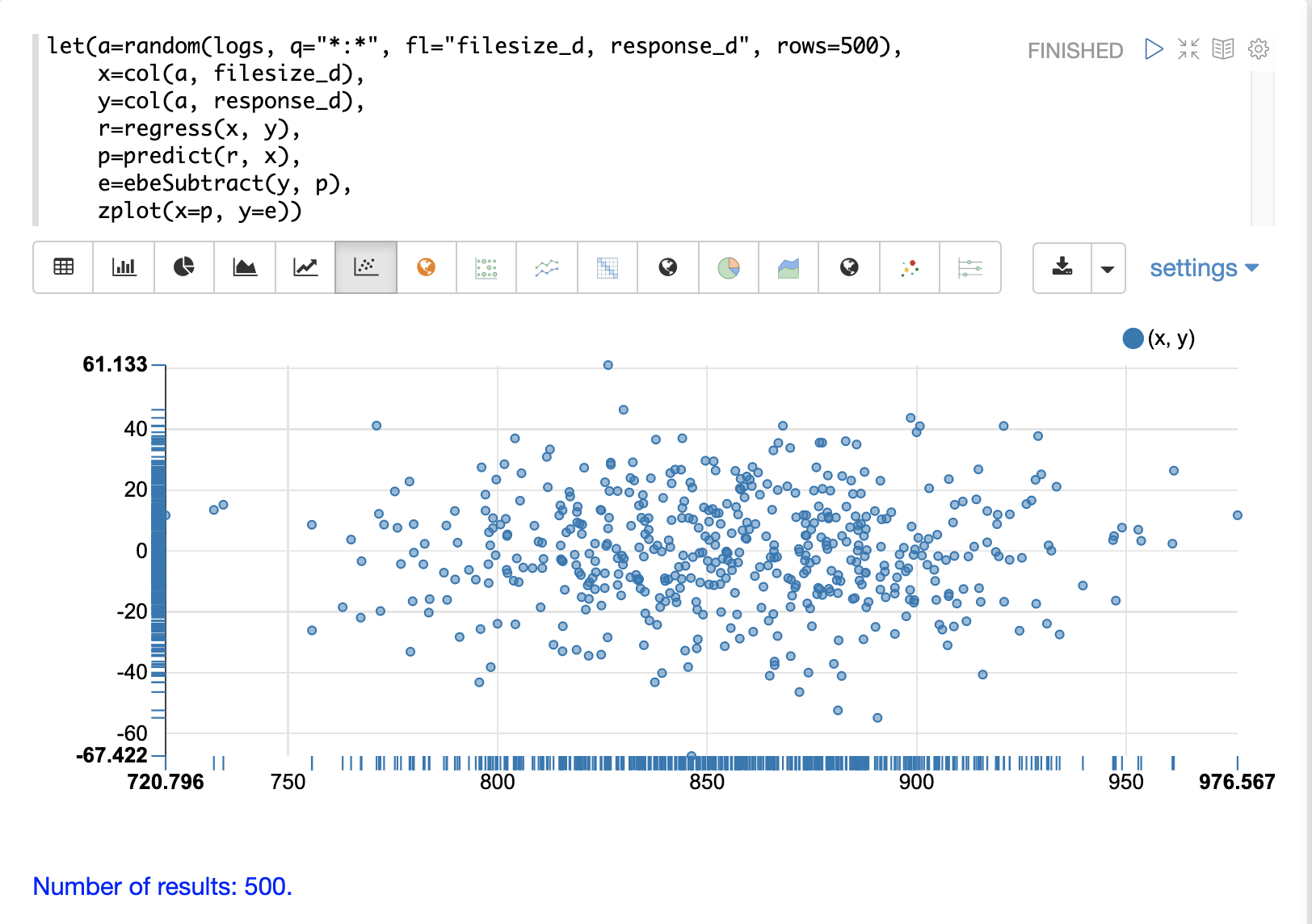
residual plot

残差图可用于解释模型的可靠性。需要注意三件事

  1. 残差看起来是否呈均值为 0 的正态分布？这使得更容易解释模型的结果，以确定误差的分布是否对于预测可以接受。这也使得更容易使用残差模型对新预测进行异常检测。

  2. 残差看起来是否是**异方差**？这意味着残差的方差在预测范围内是否相同？通过在 x 轴上绘制预测值，在 y 轴上绘制误差，我们可以看到当预测值较高时，变异性是否保持不变。如果残差是异方差的，则意味着我们可以信任模型的误差在整个预测范围内保持一致。

  3. 残差是否存在任何模式？ 如果存在，则可能数据中仍然存在需要建模的信号。

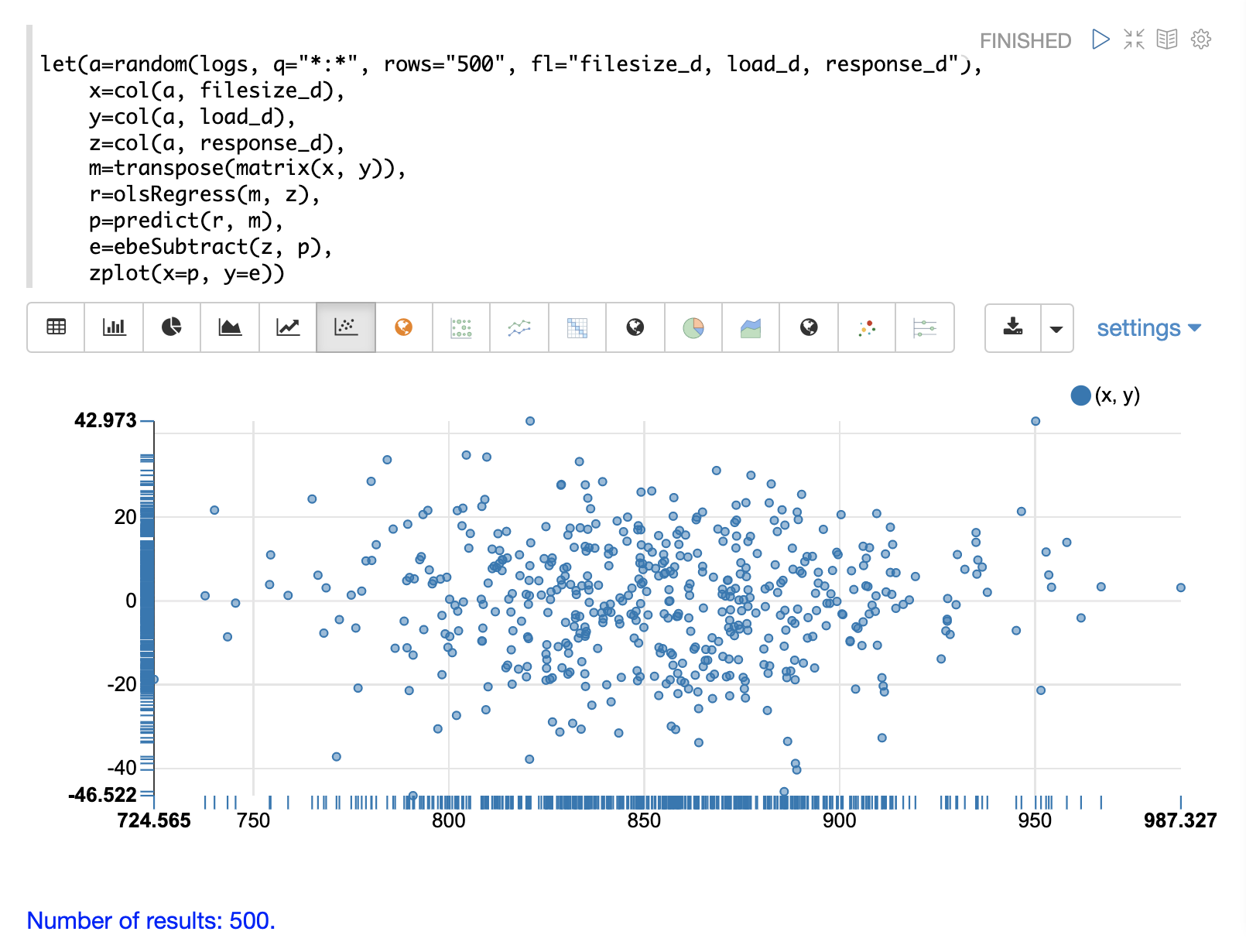
多元线性回归

olsRegress 函数执行多元线性回归分析。多元线性回归模拟两个或多个自变量与一个因变量之间的线性关系。

下面的示例通过引入一个名为 load_d 的新自变量来扩展简单线性回归的示例。 load_d 变量表示文件下载时网络的负载。

请注意，两个自变量 filesize_d 和 load_d 被向量化并存储在变量 b 和 c 中。然后，将变量 b 和 c 作为行添加到 matrix 中。然后转置该矩阵，使矩阵中的每一行代表一个包含 filesize_d 和 service_d 的观测值。然后，olsRegress 函数使用观测值矩阵作为自变量，以及存储在变量 d 中的 response_d 值作为因变量，执行多元回归分析。

let(a=random(testapp, q="*:*", rows="30000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z))

请注意，在响应中，回归分析的 RSquared 为 1。这意味着 filesize_d 和 service_d 之间的线性关系描述了 response_d 变量 100% 的变异性

{
  "result-set": {
    "docs": [
      {
        "regressionParametersStandardErrors": [
          1.7792032752524236,
          0.0000429945089590394,
          0.0008592489428291642
        ],
        "RSquared": 0.8850359458670845,
        "regressionParameters": [
          0.7318766882597804,
          0.01998298784650873,
          0.10982104952105468
        ],
        "regressandVariance": 1938.8190758686717,
        "regressionParametersVariance": [
          [
            0.014201127587649602,
            -3.326633951803927e-7,
            -0.000001732754417954437
          ],
          [
            -3.326633951803927e-7,
            8.292732891338694e-12,
            2.0407522508189773e-12
          ],
          [
            -0.000001732754417954437,
            2.0407522508189773e-12,
            3.3121477630934995e-9
          ]
        ],
        "adjustedRSquared": 0.8850282808303053,
        "residualSumSquares": 6686612.141261716
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 374
      }
    ]
  }
}

预测

predict 函数也可以用于进行多元线性回归的预测。

下面是使用多元线性回归模型和单个观测值进行单个预测的示例。该观测值是一个数组，其结构与用于构建模型的观测值矩阵的结构相匹配。在这种情况下，第一个值表示 filesize_d 为 40000，第二个值表示 load_d 为 4。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, array(40000, 4)))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "p": 801.7725344814675
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 70
      }
    ]
  }
}

predict 函数还可以对多个多元观测值进行预测。在这种情况下，将使用观测值矩阵。

在下面的示例中，用于构建多元回归模型的观测值矩阵被传递给 predict 函数，它返回一个预测数组。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, m))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "p": [
          917.7122088913725,
          900.5418518783401,
          871.7805676516689,
          822.1887964840801,
          828.0842807117554,
          785.1262470470162,
          833.2583851225845,
          802.016811579941,
          841.5253327135974,
          896.9648275225625,
          858.6511235977382,
          869.8381475112501
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

残差

一旦生成预测值，就可以使用与简单线性回归相同的方法来计算残差。

以下是一个多元线性回归后计算残差的示例。在该示例中，从存储在变量 d 中的观测值中减去存储在变量 g 中的预测值。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, m),
    e=ebeSubtract(z, p))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "e": [
          21.452271655340496,
          9.647947283595727,
          -23.02328008866334,
          -13.533046479596806,
          -16.1531952414299,
          4.966514036315402,
          23.70151322413119,
          -4.276176642246014,
          10.781062392156628,
          0.00039750380267378205,
          -1.8307638852961645
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

残差图

多元线性回归的残差图与简单线性回归的残差图相同。预测值绘制在 x 轴上，误差绘制在 y 轴上。

residual plot2

多元线性回归的残差图的解释方式与简单线性回归完全相同。