机器学习
数学表达式用户指南的这一部分介绍了机器学习函数。
距离和距离矩阵
distance 函数计算两个数值数组的距离,或计算矩阵列的距离矩阵。
有六个距离度量函数返回一个执行实际距离计算的函数
-
euclidean(默认) -
manhattan -
canberra -
earthMovers -
cosine -
haversineMeters(地理空间距离度量)
距离度量函数可以与所有支持距离度量的机器学习函数一起使用。
以下是计算两个数值数组的欧几里得距离的示例
let(a=array(20, 30, 40, 50),
b=array(21, 29, 41, 49),
c=distance(a, b))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"c": 2
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}下面使用曼哈顿距离计算距离。
let(a=array(20, 30, 40, 50),
b=array(21, 29, 41, 49),
c=distance(a, b, manhattan()))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"c": 4
},
{
"EOF": true,
"RESPONSE_TIME": 1
}
]
}
}距离矩阵
距离矩阵是可视化两个或多个向量之间距离的强大工具。
如果将矩阵作为参数传递,distance 函数将构建距离矩阵。距离矩阵是针对矩阵的列计算的。
下面的示例演示了距离矩阵与二维分面结合的强大功能。
在此示例中,使用 facet2D 函数在 nyc311 投诉数据库的字段 complaint_type_s 和 zip_s 上生成二维分面聚合。聚合每个投诉类型的前 20 名投诉类型和前 25 名邮政编码。结果是一个元组流,每个元组包含字段 complaint_type_s、zip_s 和该对的计数。
然后使用 pivot 函数将字段透视到以 zip_s 字段作为行,complaint_type_s 字段作为列的矩阵中。count(*) 字段填充矩阵单元格中的值。
然后使用 distance 函数使用 cosine 距离计算矩阵列的距离矩阵。这将生成一个距离矩阵,该矩阵显示基于投诉类型出现的邮政编码,投诉类型之间的距离。
最后,使用 zplot 函数将距离矩阵绘制为热图。请注意,热图已配置为使颜色强度随着向量之间的距离减小而增加。
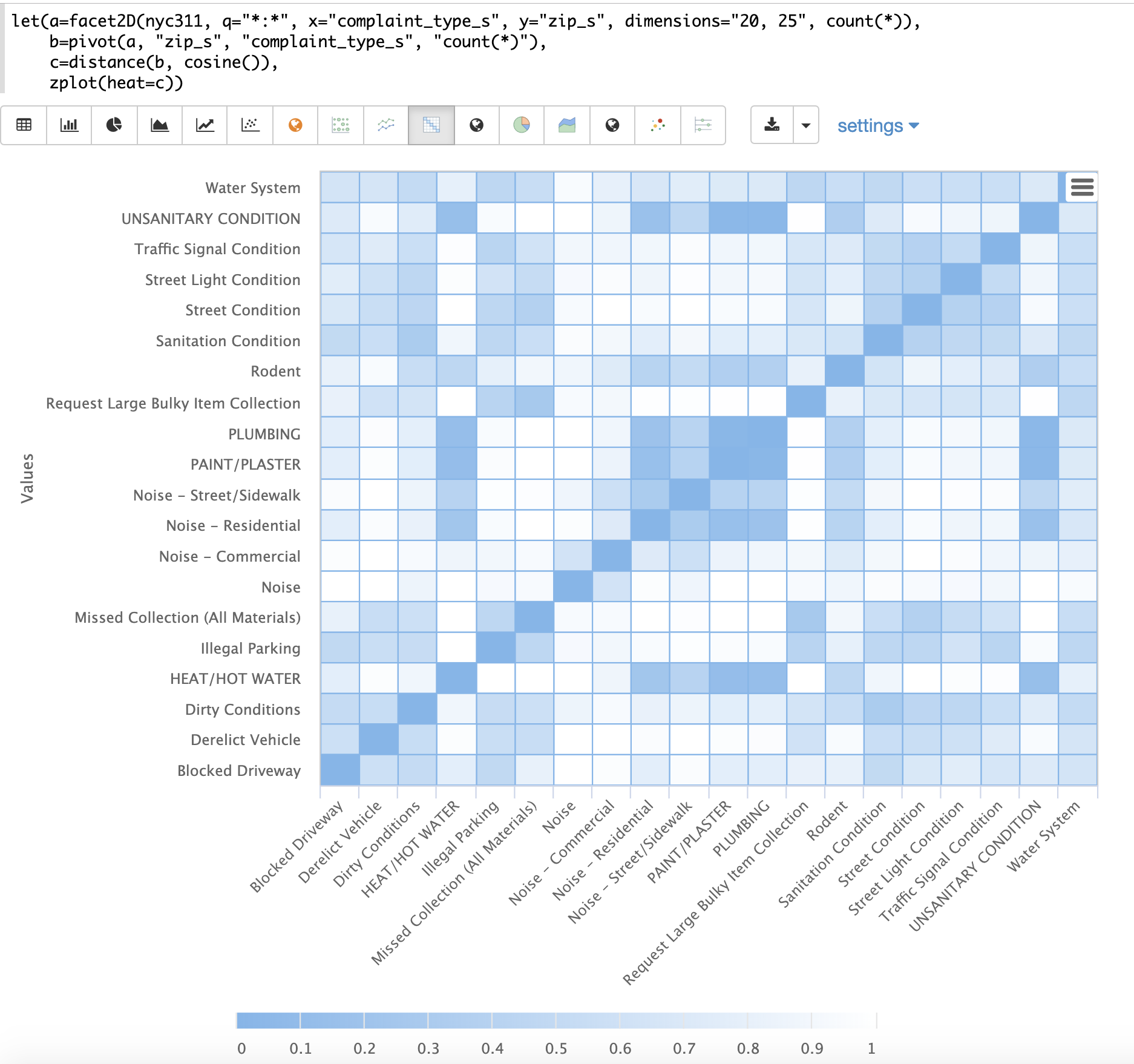
热图是交互式的,因此将鼠标悬停在其中一个单元格上会弹出该单元格的值。
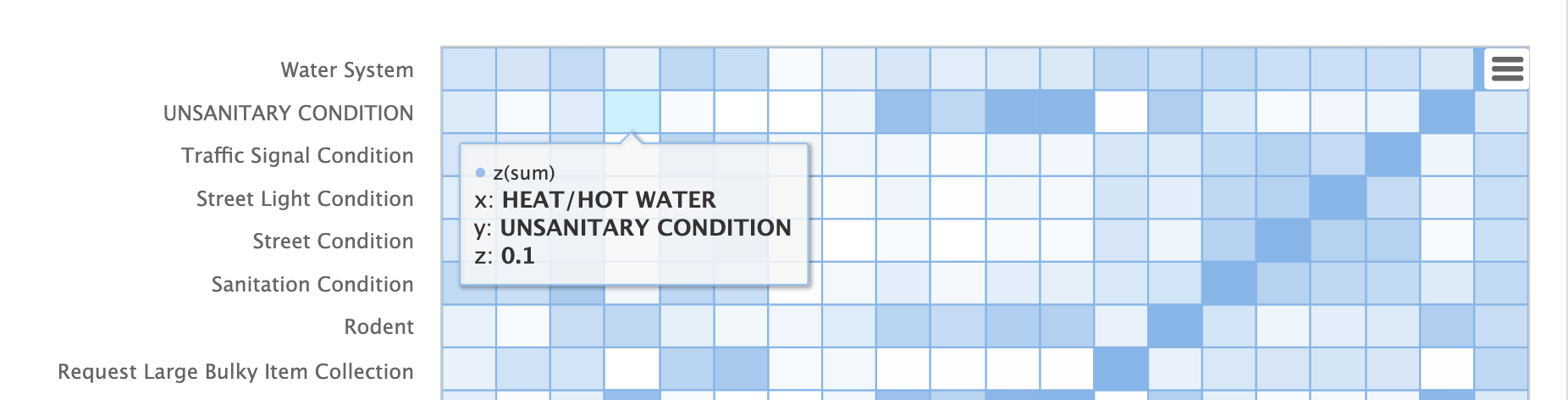
请注意,HEAT/HOT WATER 和 UNSANITARY CONDITION 投诉的余弦距离为 0.1(四舍五入到最接近的十分之一)。
K 最近邻 (KNN)
knn 函数使用搜索向量搜索矩阵的行,并返回 k 个最近邻的矩阵。这允许在结果集上进行二次向量搜索。
knn 函数支持通过提供以下距离度量函数之一来更改距离度量
-
euclidean(默认) -
manhattan -
canberra -
earthMovers -
cosine -
haversineMeters(地理空间距离度量)
下面的示例演示如何在聚合结果集上执行二次搜索。该示例的目标是在 nyc311 投诉数据库中找到与邮政编码 10280 具有相似投诉类型的邮政编码。
示例中的第一步是使用 facet2D 函数对 zip_s 和 complaint_type_s 字段执行二维聚合。在本例中,计算了曼哈顿行政区的前 119 个邮政编码以及每个邮政编码的前 5 种投诉类型。结果是一个元组列表,每个元组包含 zip_s、complaint_type_s 和组合的 count(*)。
然后,使用 pivot 函数将元组列表透视为矩阵。本例中的 pivot 函数返回一个矩阵,其中行是邮政编码,列是投诉类型。元组中的 count(*) 字段填充矩阵的单元格。此矩阵将用作辅助搜索矩阵。
下一步是找到 10280 邮政编码的向量。这在示例中分三步完成。第一步是使用 getRowLabels 函数从矩阵中检索行标签。在本例中,行标签是由 pivot 函数填充的邮政编码。然后,使用 indexOf 函数查找行标签列表中 “10280” 邮政编码的索引。然后,使用 rowAt 函数从矩阵中返回该索引处的向量。此向量是搜索向量。
现在我们有了一个矩阵和搜索向量,我们可以使用 knn 函数执行搜索。在本例中,knn 函数使用 K 为 5 和 余弦距离来搜索具有搜索向量的矩阵。余弦距离适用于比较稀疏向量,在本例中就是这种情况。knn 函数返回一个矩阵,其中包含与搜索向量最接近的 5 个邻居。
knn 函数填充返回矩阵的行和列标签,还为矩阵的每个行添加一个距离向量作为属性。
在本例中,zplot 函数使用 getRowLabels 和 getAttribute 函数提取行标签和距离向量。topFeatures 函数用于根据每列的计数提取每个邮政编码向量的前 5 个列标签。然后,zplot 以可以在 Zeppelin-Solr 中以表格形式可视化的格式输出数据。
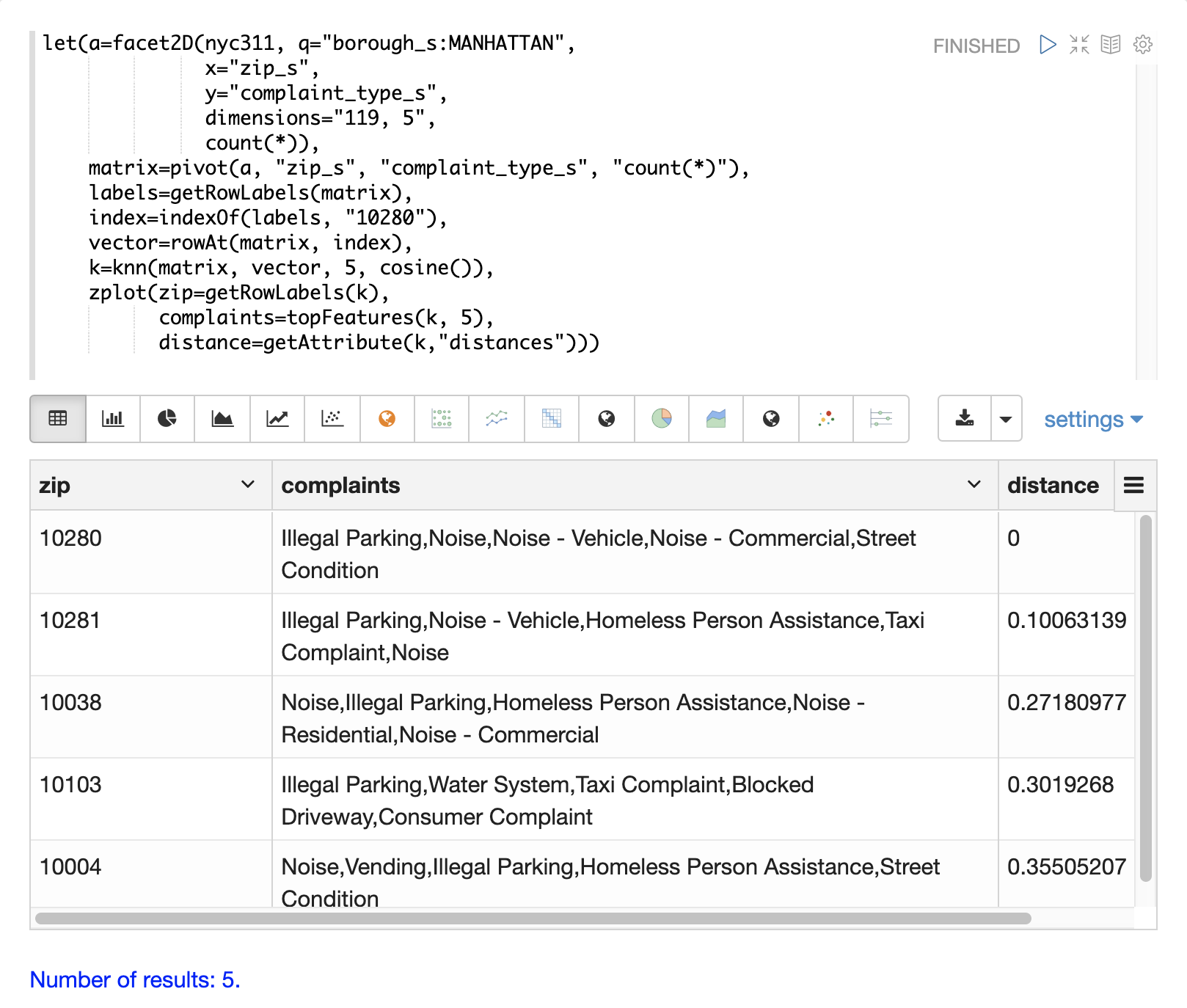
上表显示了 knn 函数返回的每个邮政编码以及投诉列表和距离。这些是基于其前 5 种投诉类型与 10280 邮政编码最相似的邮政编码。
K 最近邻回归
K 最近邻回归是一种非线性、二元和多元回归方法。KNN 回归是一种惰性学习技术,这意味着它不会预先将模型拟合到训练集。相反,整个观测值和结果的训练集都保存在内存中,并通过平均 k 个最近邻居的结果进行预测。
knnRegress 函数用于执行最近邻回归。
二维非线性回归
下面的示例显示了应用于二维散点图的 KNN 回归的回归图。
在此示例中,random 函数用于从包含两个字段 filesize_d 和 eresponse_d 的 logs 集合中抽取 500 个随机样本。然后使用存储在变量 x 中的向量中的 filesize_d 字段和存储在变量 y 中的 eresponse_d 向量对样本进行向量化。然后应用 knnRegress 函数,将 20 作为最近邻参数,返回一个可用于预测值的 KNN 函数。然后在 KNN 函数上调用 predict 函数以预测原始 x 向量的值。最后,zplot 用于绘制原始 x 和 y 向量以及预测值。
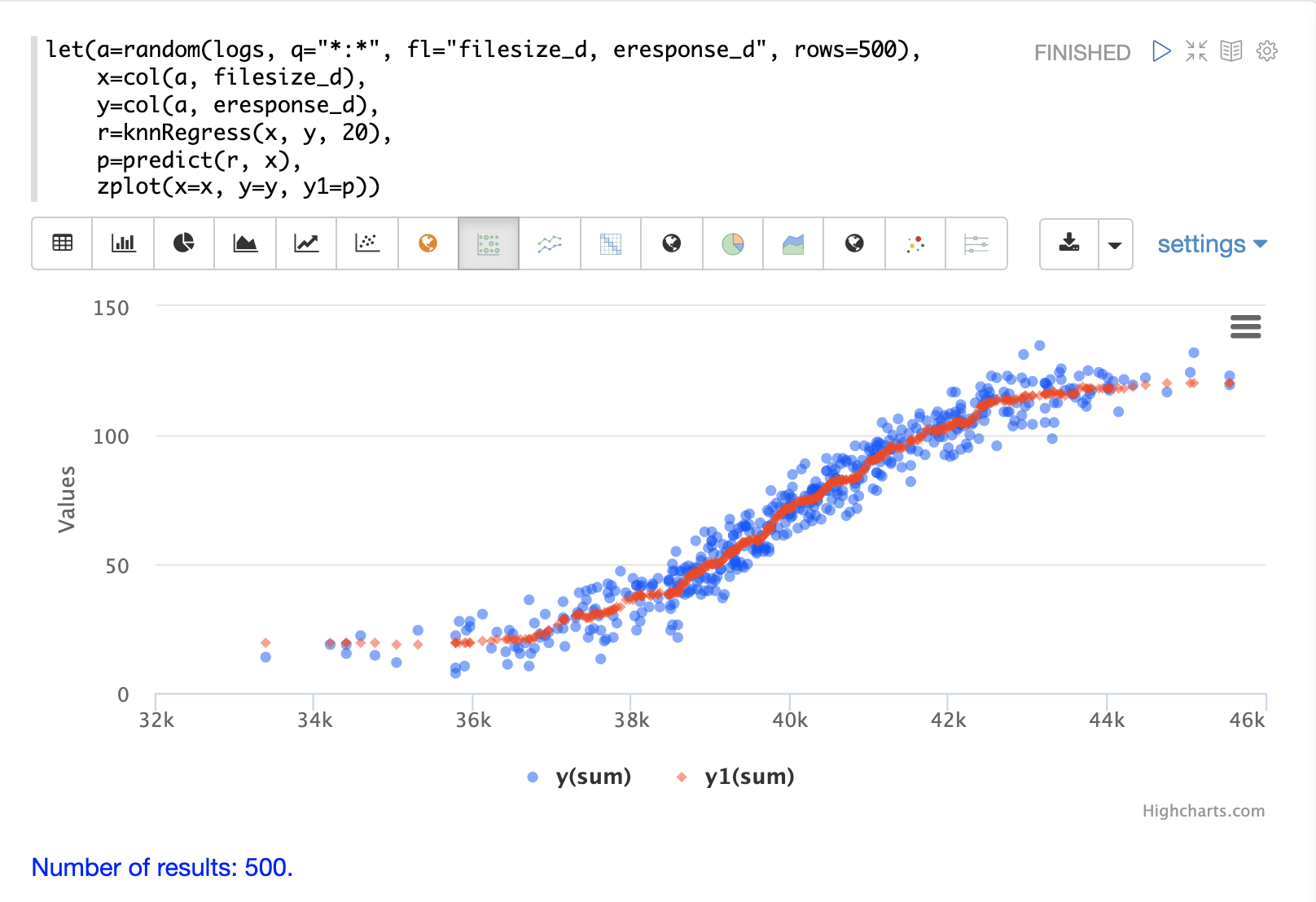
请注意,回归图显示了 filesize_d 字段和 eresponse_d 字段之间的非线性关系。另请注意,KNN 回归在散点图中绘制了一条非线性曲线。K(最近邻居)的大小越大,线条越平滑。
多元非线性回归
knnRegress 函数也是用于多元非线性回归的强大而灵活的工具。
在下面的示例中,使用旨在分析和预测葡萄酒质量的数据库执行多元回归。该数据库包含近 1600 条记录,其中包含 9 个葡萄酒质量预测指标:pH 值、酒精含量、固定酸度、硫酸盐、密度、游离二氧化硫、挥发性酸度、柠檬酸、残留糖。还有一个名为质量的字段分配给每种葡萄酒,范围从 3 到 8。
KNN 回归可用于预测包含预测变量值的向量的葡萄酒质量。
在示例中,对 redwine 集合执行搜索以返回观测值数据库中的所有行。然后将质量字段和预测变量字段读取到向量中并设置为变量。
将预测变量作为行添加到矩阵中,然后将其转置,以便矩阵中的每一行都包含一个包含 9 个预测变量值的观测值。这是我们的观测矩阵,已分配给变量 obs。
然后,knnRegress 函数使用质量结果对观测值进行回归。在本示例中,K 的值设置为 5,因此将使用 5 个最近邻居的平均质量来计算质量。
然后,使用 predict 函数为整个观测值集生成预测向量。这些预测将用于确定 KNN 回归在观测数据上的表现如何。
然后,通过从观测质量中减去预测质量来计算回归的误差或残差。ebeSubtract 函数用于执行两个向量之间的元素逐个减法。
最后,zplot 函数格式化预测和误差,以可视化残差图。
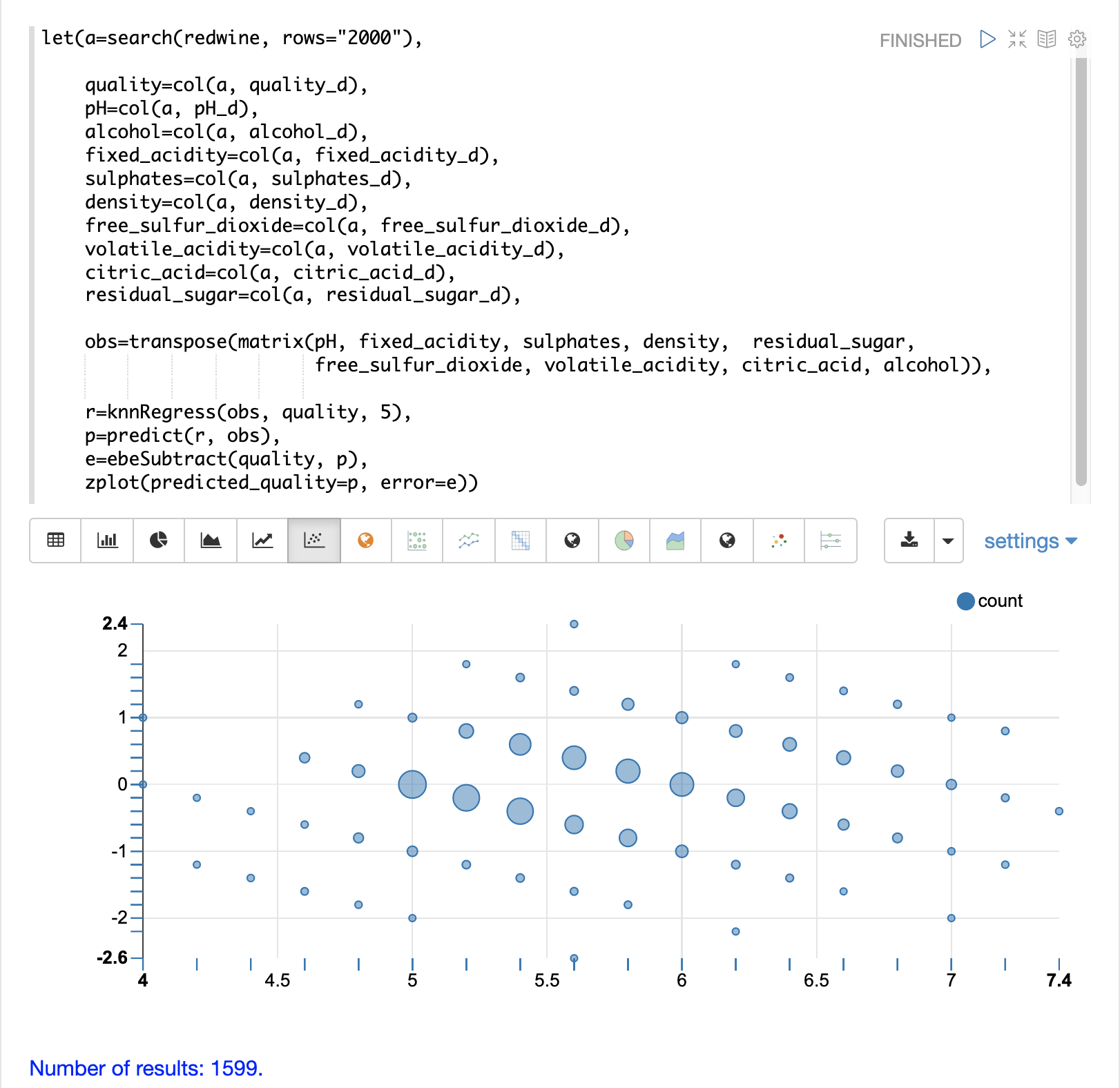
残差图在 x 轴上绘制预测值,在 y 轴上绘制预测的误差。散点图显示了误差如何在整个预测范围内分布。
可以解释残差图以了解 KNN 回归在训练数据上的表现如何。
-
该图显示预测误差似乎在零上下均匀分布。随着它接近零,误差的密度增加。气泡大小反映了图中特定点的误差密度。这为模型的误差分布提供了一种直观的感觉。
-
该图还可视化了误差在整个预测范围内的方差。这提供了对 KNN 预测是否在整个预测范围内具有相似误差方差的直观理解。
还可以使用直方图可视化残差,以更好地了解残差分布的形状。下面的示例显示了与上面相同的 KNN 回归,并绘制了误差分布图。
在该示例中,zplot 函数用于绘制残差的 empiricalDistribution 函数,并使用 11 个直方图箱。
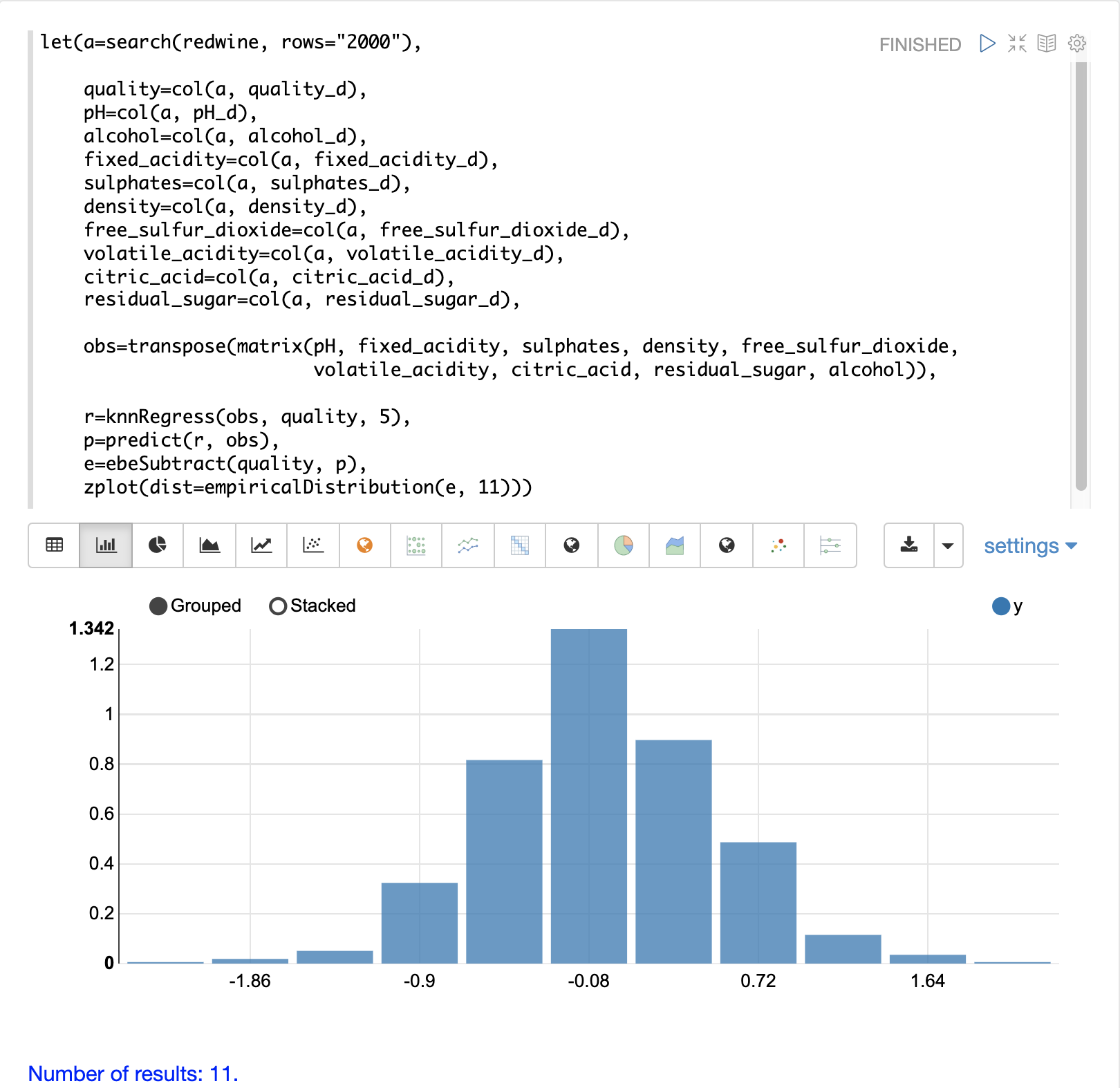
请注意,误差遵循以接近 0 为中心的钟形曲线。从该图中我们可以看到获得 -1 到 1 之间的预测误差的概率非常高。
其他 KNN 回归参数
knnRegression 函数有三个附加参数,使其适用于许多不同的回归场景。
-
任何距离度量都可以通过将函数添加到调用中来用于回归。这允许对稀疏向量 (
cosine)、密集向量和地理空间纬度/经度向量 (haversineMeters) 进行回归分析。示例语法
r=knnRegress(obs, quality, 5, cosine()), -
可以使用
robust命名参数来执行对结果中的异常值具有鲁棒性的回归分析。当使用robust参数时,将使用 k 个最近邻居的中值结果,而不是平均值。示例语法
r=knnRegress(obs, quality, 5, robust="true"), -
可以使用
scale命名参数在预测时缩放观测值和搜索向量的列。当特征列的比例不同导致距离计算过多地权重于较大的列时,这可以提高 KNN 回归的性能。示例语法
r=knnRegress(obs, quality, 5, scale="true"),
knnSearch
knnSearch 函数基于文本相似性返回文档的 k 个最近邻居。在底层,knnSearch 函数使用 Solr 的 More Like This 查询解析器。此功能使用搜索引擎的查询、术语统计、评分和排名功能,在大规模分布式索引上执行快速、最近邻搜索以查找相似文档。
此搜索的结果可以直接使用,也可以为机器学习操作(例如辅助 KNN 向量搜索)提供候选对象。
下面的示例显示了电影评论数据集上的 knnSearch 函数。该搜索返回与基于 review_t 字段的相似性与特定文档 ID (83e9b5b0…) 最相似的 50 个文档。mindf 和 maxdf 指定用于执行搜索的术语的最小和最大文档频率。这些参数可以通过消除高频术语来加快查询速度,还可以通过从搜索中删除噪声术语来提高准确性。
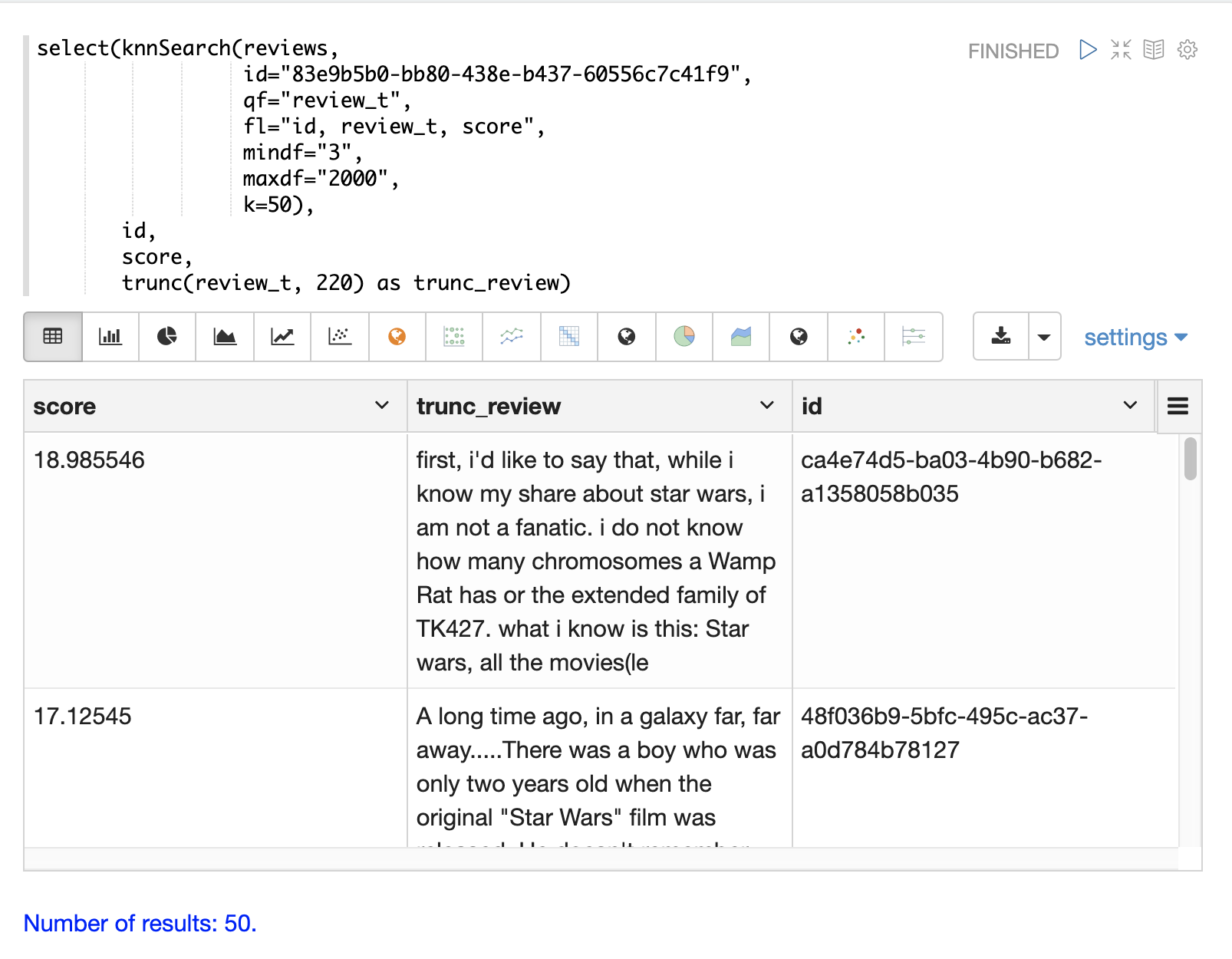
在此示例中,使用 select 函数截断输出中的评论为 220 个字符,以便更易于在表格中阅读。 |
DBSCAN
DBSCAN 聚类是一种强大的基于密度的聚类算法,特别适用于地理空间聚类。DBSCAN 使用两个参数来将结果集过滤到特定密度的聚类
-
eps(Epsilon):定义要被视为邻居的点之间的距离 -
min点:返回的聚类中所需的最小点数。
二维聚类可视化
zplot 函数通过使用 clusters 命名参数直接支持绘制二维聚类。
下面的示例使用 DBSCAN 聚类和聚类可视化来查找纽约市 311 投诉数据库中老鼠目击事件地图上的热点。
在本例中,random 函数从 nyc311 集合中抽取记录样本,其中投诉描述与“老鼠目击事件”匹配,并且记录中填充了纬度。然后将纬度和经度字段向量化并作为行添加到矩阵中。将矩阵转置,以便每一行都包含一个纬度、经度点。然后,使用 dbscan 函数对纬度和经度点进行聚类。请注意,示例中的 dbscan 函数有四个参数。
-
obs:纬度/经度点的观测矩阵 -
eps:被视为聚类的点之间的距离。在本示例中为 100 米。 -
min points:函数要返回的聚类中的最小点数。在本示例中为5。 -
distance measure:用于确定点之间距离的可选距离度量。默认值为欧几里得距离。本例使用haversineMeters,它返回以米为单位的距离,这对于地理空间用例更有意义。
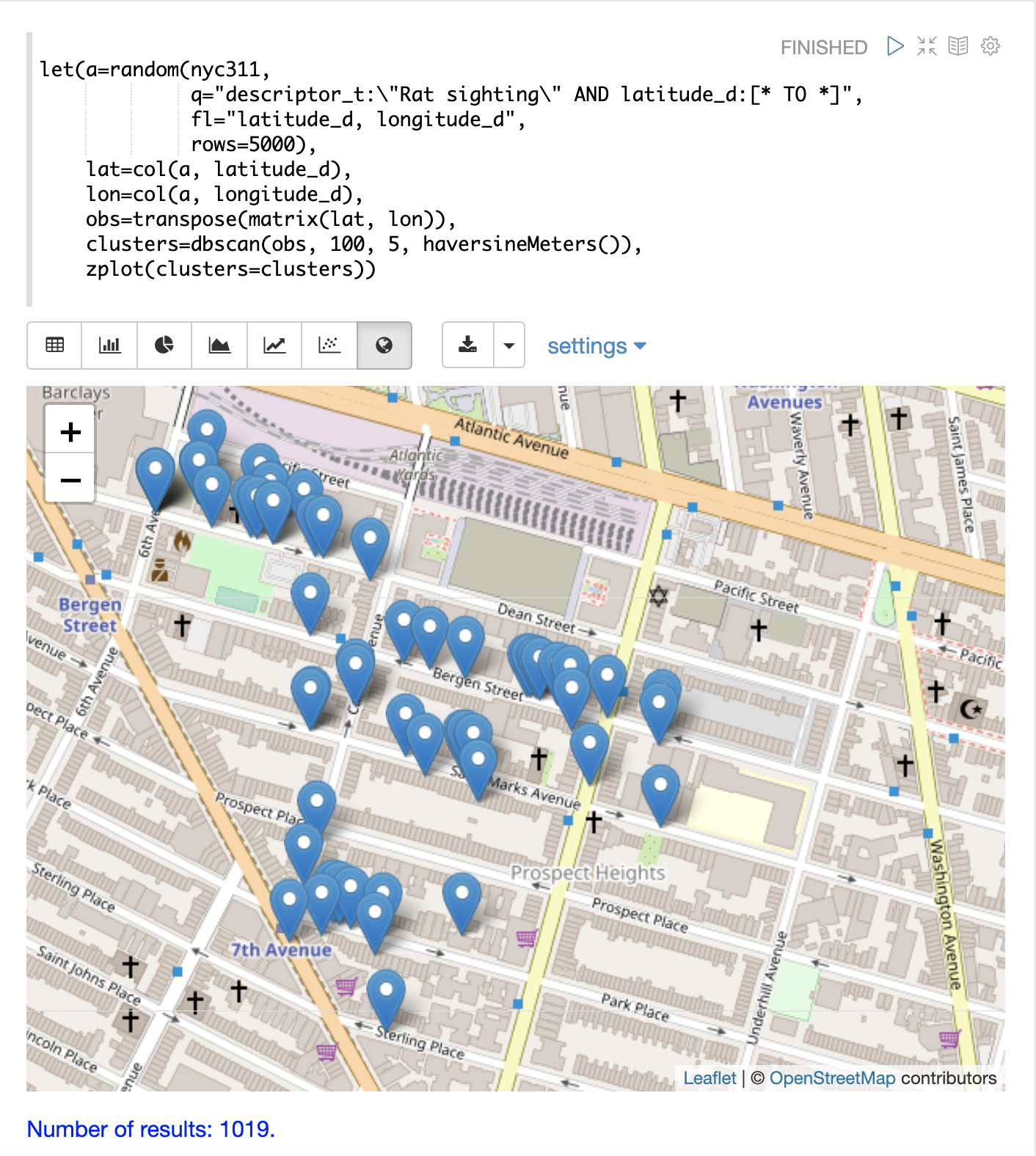
最后,zplot 函数用于使用 Zeppelin-Solr 在地图上可视化聚类。下面的地图已放大到布鲁克林一个老鼠目击事件密度很高的特定区域。
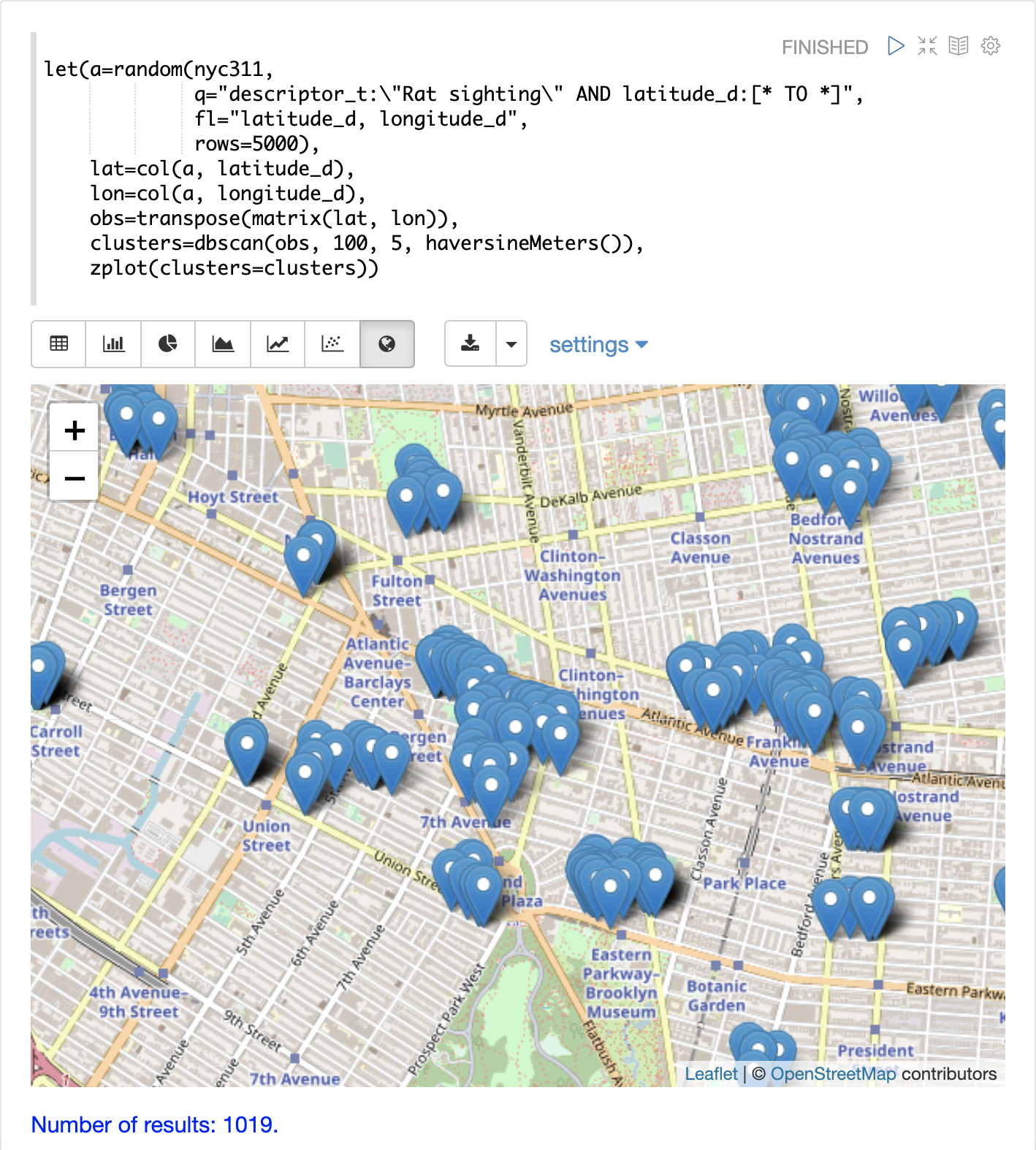
在可视化中请注意,仅从 5000 个样本中返回了 1019 个点。这是 DBSCAN 算法过滤不符合聚类标准的记录的能力。绘制的点都属于明确定义的聚类。
可以进一步放大地图可视化以探索特定聚类的位置。下面的示例显示了放大到密集聚类区域的区域。
K均值聚类
kmeans 函数对矩阵的行执行 k 均值聚类。一旦聚类完成,有许多有用的函数可用于检查和可视化聚类和质心。
聚类散点图
在这个例子中,我们将再次对老鼠目击事件的 2D 经纬度点进行聚类。但与 DBSCAN 示例不同,k 均值聚类本身不执行任何噪声降低。因此,为了减少噪声,从数据中选择的随机样本比用于 DBSCAN 示例的要小。
我们将看到,抽样本身是一个强大的噪声降低工具,有助于可视化聚类密度。这是因为样本更有可能从较高密度的聚类中抽取,而从较低密度的聚类中抽取的可能性较低。
在本例中,random 函数从 nyc311(投诉数据库)集合中抽取 1500 条记录的样本,其中投诉描述与“老鼠目击”匹配,并且记录中填充了纬度。然后将纬度和经度字段向量化并作为行添加到矩阵中。矩阵被转置,因此每一行包含一个纬度、经度点。然后使用 kmeans 函数将纬度和经度点聚类为 21 个聚类。最后,使用 zplot 函数将聚类可视化为散点图。
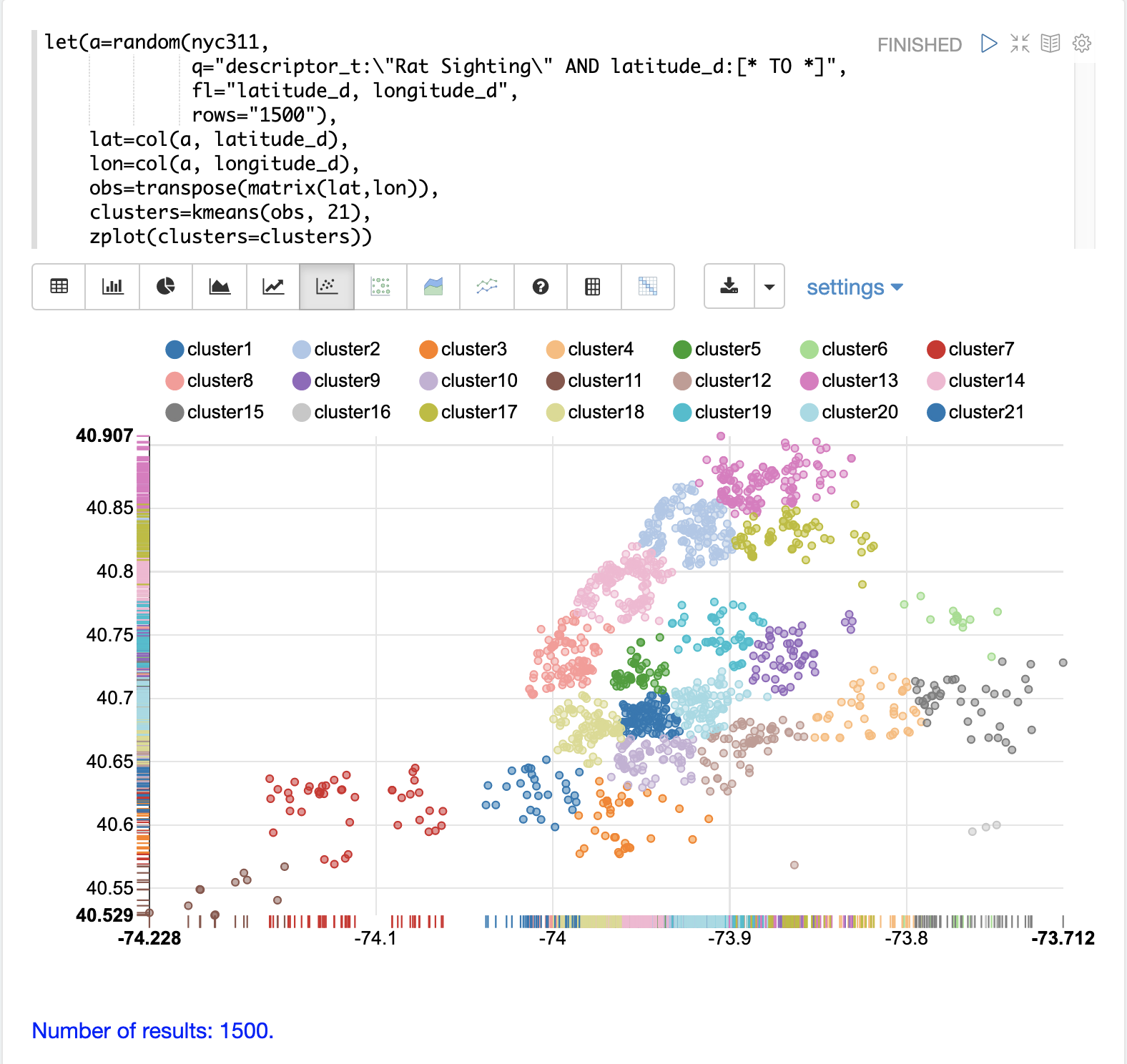
上面的散点图显示了每个经纬度点在欧几里得平面上的绘制,横轴为经度,纵轴为纬度。如果您知道纽约市的行政区,则该图足够密集,可以看到不同行政区的轮廓。
每个聚类以不同的颜色显示。此图提供了对纽约市五个行政区老鼠目击事件密度的有趣见解。例如,它突出了布鲁克林 cluster1 中密集的目击事件聚类,周围是密度较低但仍为高活动的聚类。
绘制质心
然后可以在地图上绘制每个聚类的质心,以可视化聚类的中心。在下面的示例中,使用 getCentroids 函数从聚类中提取质心,该函数返回质心的矩阵。
质心矩阵包含 2D 经纬度点。然后可以使用 colAt 函数从矩阵中按索引提取纬度和经度列,以便可以使用 zplot 绘制它们。下面使用地图可视化来显示质心。
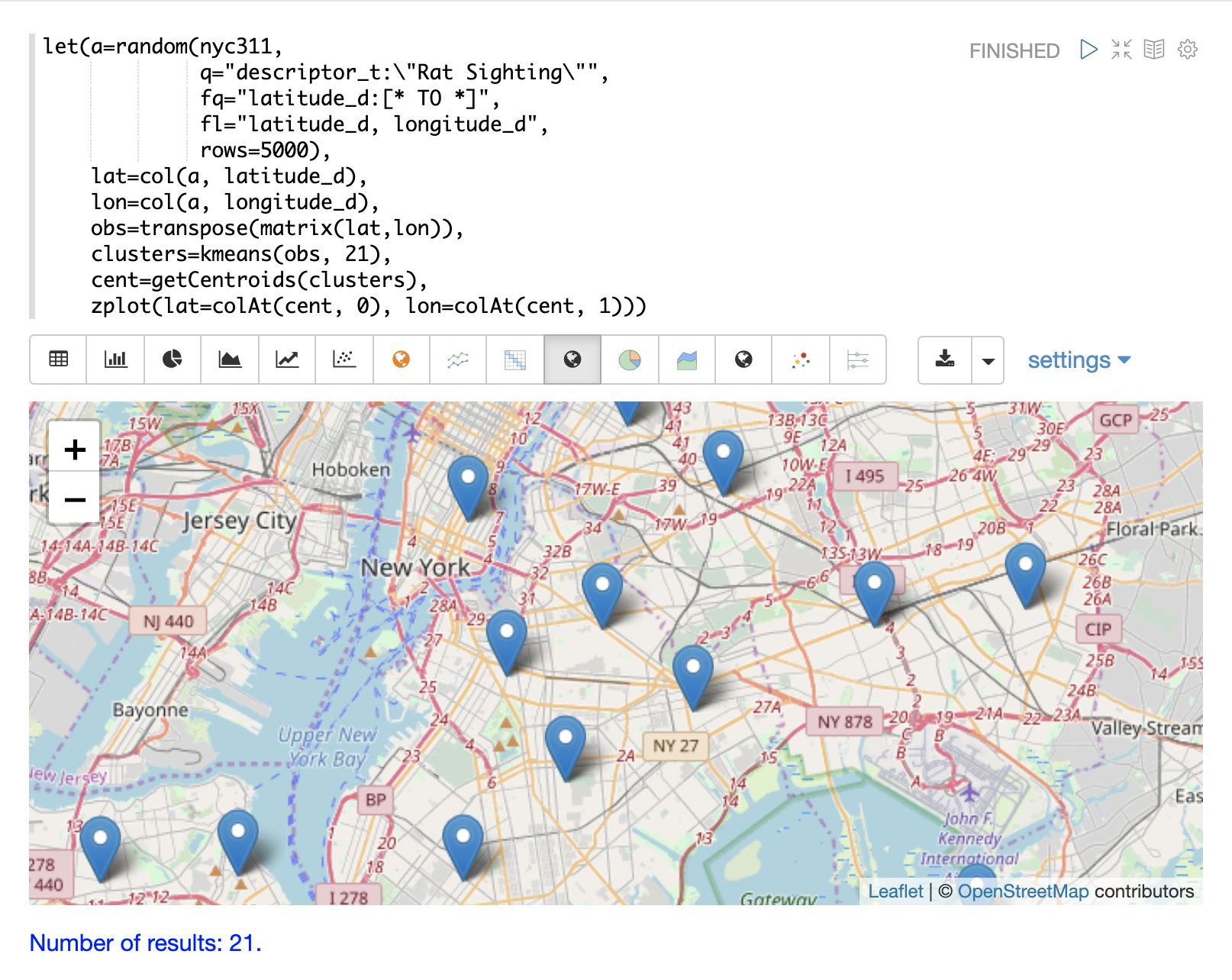
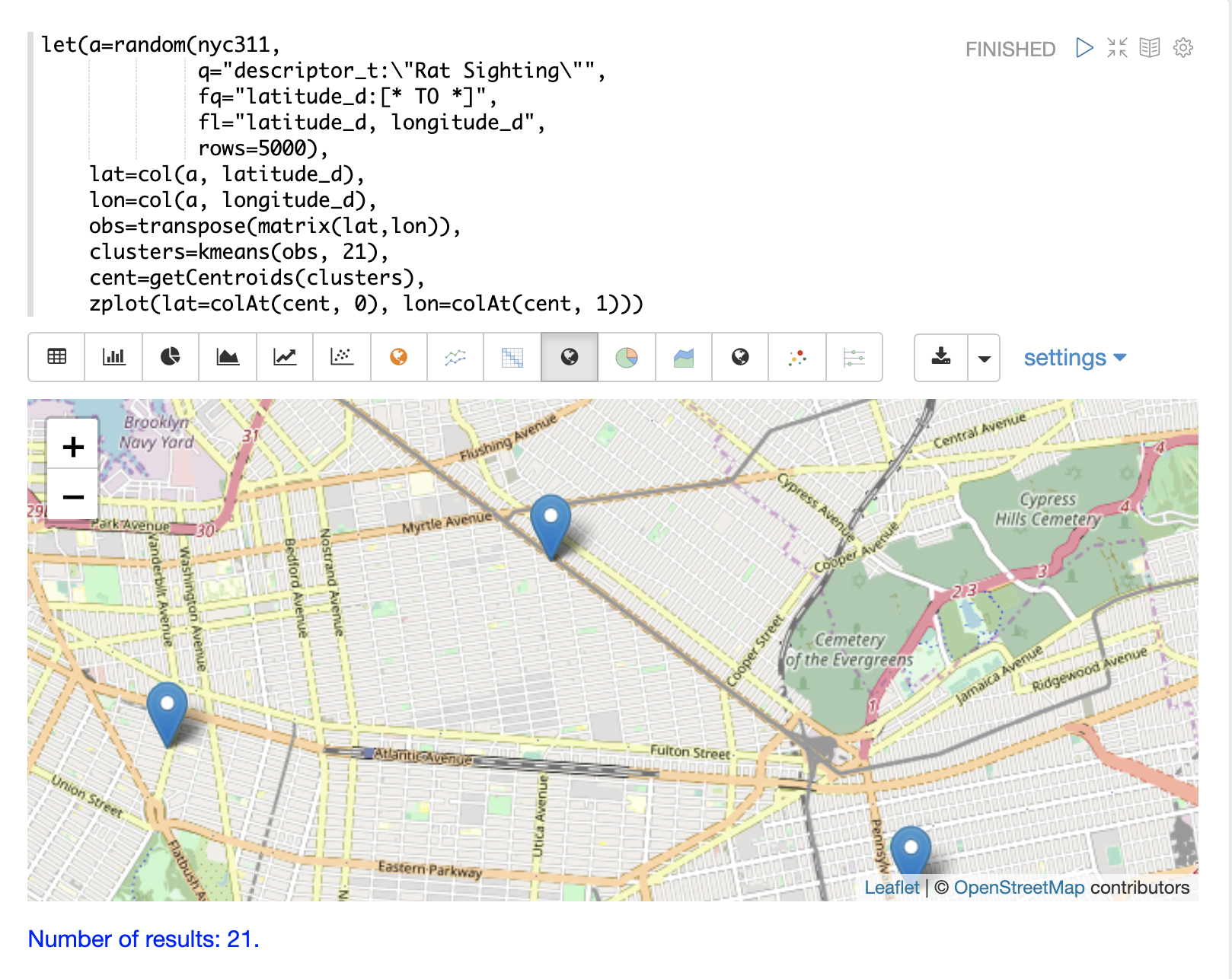
然后可以缩放地图以更仔细地查看聚类散点图中显示的高密度区域中的质心。
短语提取
K 均值聚类生成质心或原型向量,可用于表示每个聚类。在此示例中,提取质心的关键特征以表示 TF-IDF 词向量聚类的关键短语。
| 下面的示例使用 TF-IDF 词向量。“文本分析和词向量”部分提供了对这些功能的完整解释。 |
在该示例中,search 函数返回 review_t 字段与短语“star wars”匹配的文档。对结果集运行 select 函数,并应用 analyze 函数,该函数使用附加到模式字段 text_bigrams 的分析器来重新分析 review_t 字段。此分析器返回双字母组合,然后将这些双字母组合注释到名为 terms 的字段中的文档。
然后 termVectors 函数从 terms 字段中存储的双字母组合创建 TD-IDF 词向量。然后使用 kmeans 函数将双字母组合词向量聚类为 5 个聚类。最后,从质心中提取前 5 个特征并返回。请注意,这些特征都是具有语义意义的双字母组合短语。
let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
id,
analyze(review_t, text_bigrams) as terms),
vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
clusters=kmeans(vectors, 5),
centroids=getCentroids(clusters),
phrases=topFeatures(centroids, 5))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"phrases": [
[
"empire strikes",
"rebel alliance",
"princess leia",
"luke skywalker",
"phantom menace"
],
[
"original star",
"main characters",
"production values",
"anakin skywalker",
"luke skywalker"
],
[
"carrie fisher",
"original films",
"harrison ford",
"luke skywalker",
"ian mcdiarmid"
],
[
"phantom menace",
"original trilogy",
"harrison ford",
"john williams",
"empire strikes"
],
[
"science fiction",
"fiction films",
"forbidden planet",
"character development",
"worth watching"
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 46
}
]
}
}多 K 均值聚类
K 均值聚类会根据质心的初始位置产生不同的结果。K 均值的速度足够快,可以执行多次试验,以便可以选择最佳结果。
multiKmeans 函数运行给定次数试验的 k 均值聚类算法,并根据哪个试验产生最低的簇内方差来选择最佳结果。
下面的示例与短语提取示例相同,不同之处在于它使用 15 次试验的 multiKmeans,而不是 kmeans 函数的单次试验。
let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
id,
analyze(review_t, text_bigrams) as terms),
vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
clusters=multiKmeans(vectors, 5, 15),
centroids=getCentroids(clusters),
phrases=topFeatures(centroids, 5))此表达式返回以下响应
{
"result-set": {
"docs": [
{
"phrases": [
[
"science fiction",
"original star",
"production values",
"fiction films",
"forbidden planet"
],
[
"empire strikes",
"princess leia",
"luke skywalker",
"phantom menace"
],
[
"carrie fisher",
"harrison ford",
"luke skywalker",
"empire strikes",
"original films"
],
[
"phantom menace",
"original trilogy",
"harrison ford",
"character development",
"john williams"
],
[
"rebel alliance",
"empire strikes",
"princess leia",
"original trilogy",
"luke skywalker"
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 84
}
]
}
}模糊 K 均值聚类
fuzzyKmeans 函数是一种软聚类算法,允许将向量分配给多个聚类。fuzziness 参数是 1 和 2 之间的值,它确定聚类分配的模糊程度。
执行聚类后,可以对聚类结果调用 getMembershipMatrix 函数,以返回描述每个向量聚类成员资格概率的矩阵。此矩阵可用于了解聚类之间的关系。
在下面的示例中,使用 fuzzyKmeans 对与短语“star wars”匹配的电影评论进行聚类。但是,不是查看聚类或质心,而是使用 getMembershipMatrix 来返回每个文档的成员资格概率。成员资格矩阵由每个被聚类的向量的行组成。矩阵中每个聚类都有一个列。矩阵中的值包含特定向量属于特定聚类的概率。
在示例中,然后使用 distance 函数从成员资格矩阵的列中创建距离矩阵。然后使用 zplot 函数将距离矩阵可视化为热图。
在示例中,cluster1 和 cluster5 之间的聚类距离最短。可以对两个聚类中的特征进行进一步分析,以了解 cluster1 和 cluster5 之间的关系。
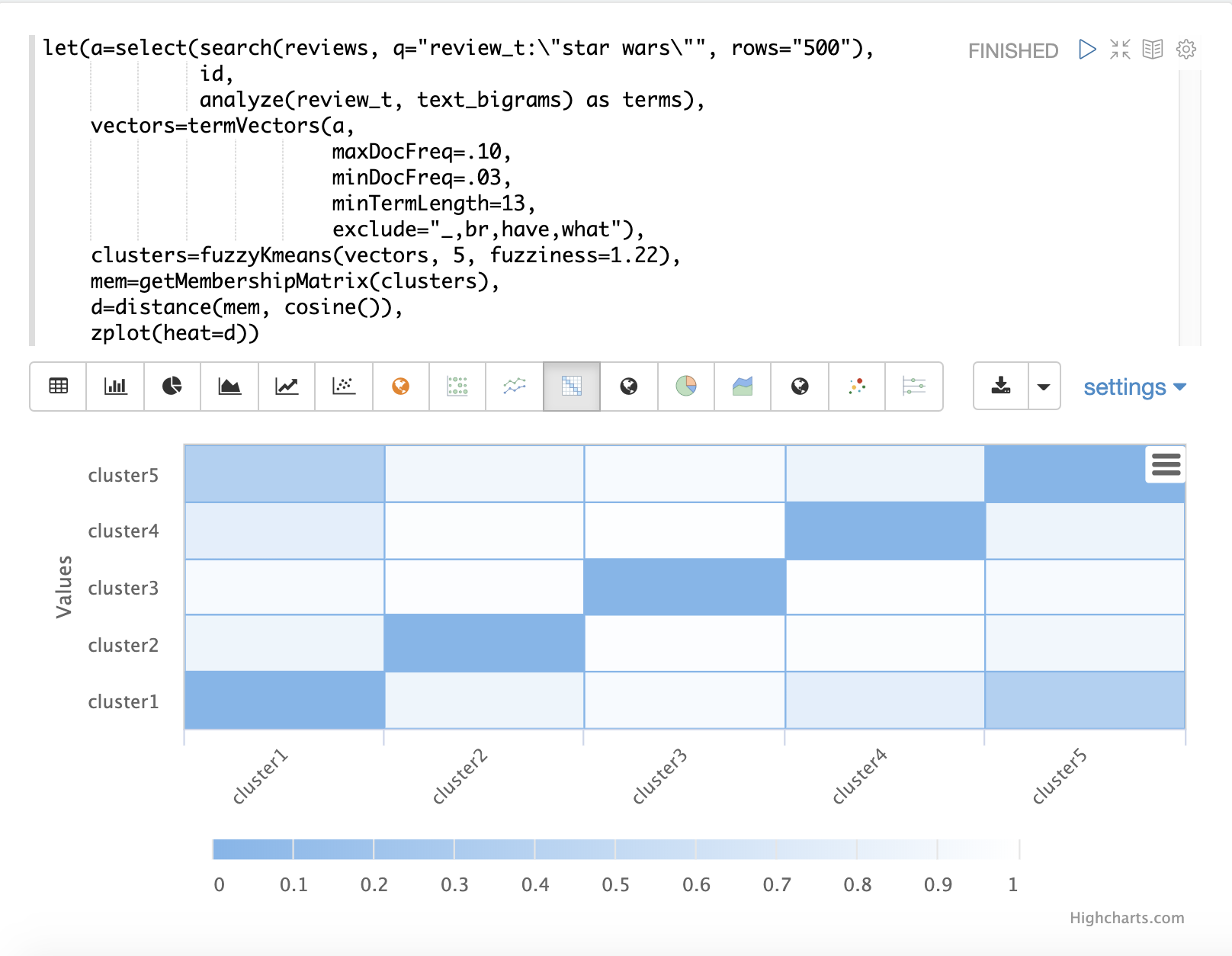
| 热图已配置为随着距离缩短而增加颜色强度。 |
特征缩放
在执行机器学习操作之前,通常需要缩放特征向量,以便可以在相同的尺度上进行比较。
下面的所有缩放函数都在向量和矩阵上运行。在矩阵上运行时,将缩放矩阵的行。
Min/Max 缩放
minMaxScale 函数在最小值和最大值之间缩放向量或矩阵。默认情况下,如果未提供最小值/最大值,则它将在 0 和 1 之间缩放。
下面是正弦波的图,在将其缩放到 -5 和 5 之间之前和之后,振幅为 1。
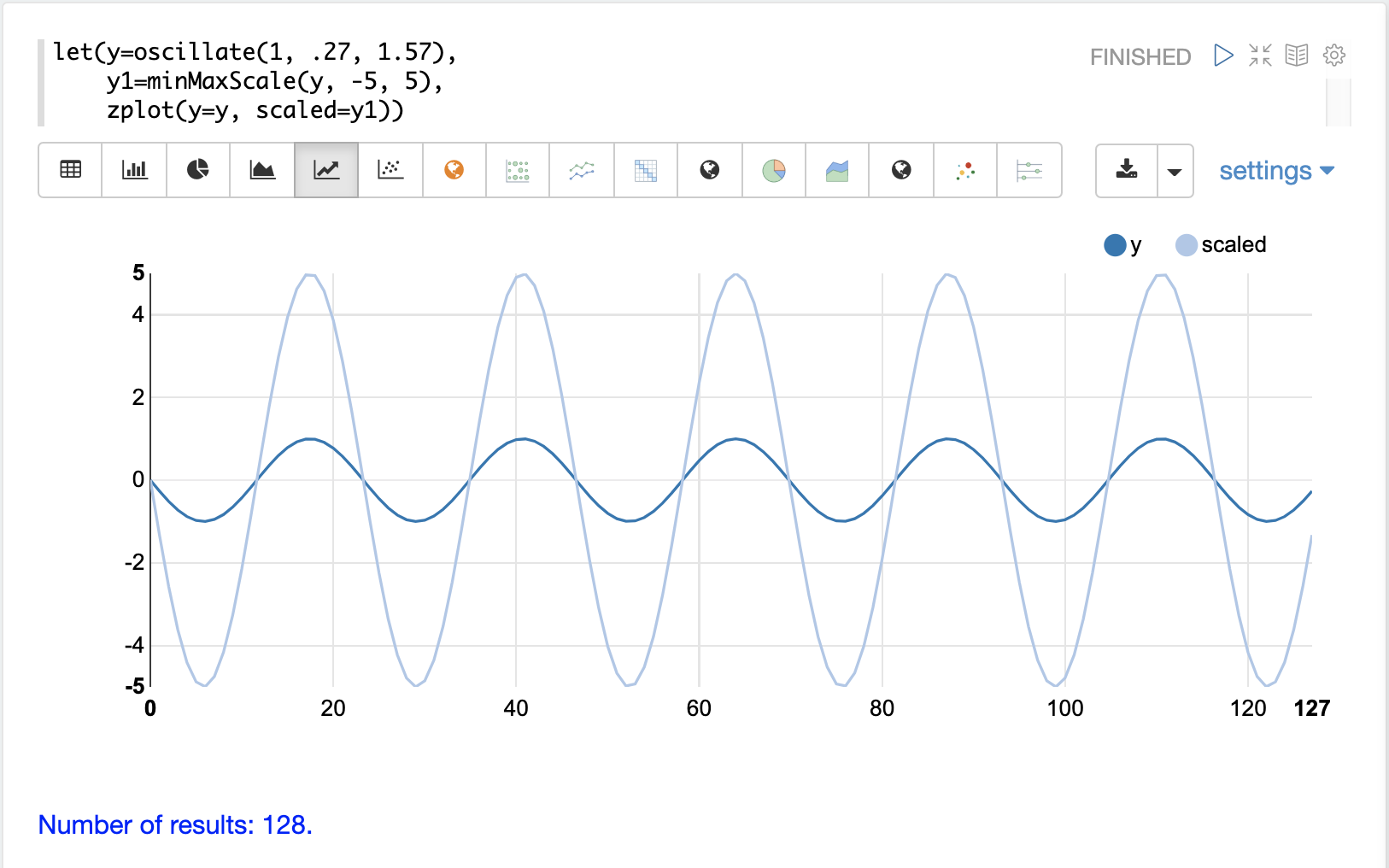
下面是一个在 0 和 1 之间对矩阵进行最小/最大缩放的简单示例。请注意,一旦将向量置于同一尺度,它们就相同了。
let(a=array(20, 30, 40, 50),
b=array(200, 300, 400, 500),
c=matrix(a, b),
d=minMaxScale(c))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"d": [
[
0,
0.3333333333333333,
0.6666666666666666,
1
],
[
0,
0.3333333333333333,
0.6666666666666666,
1
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}标准化
standardize 函数缩放向量,使其均值为 0,标准差为 1。
下面是正弦波的图,在标准化之前和之后,振幅为 1。
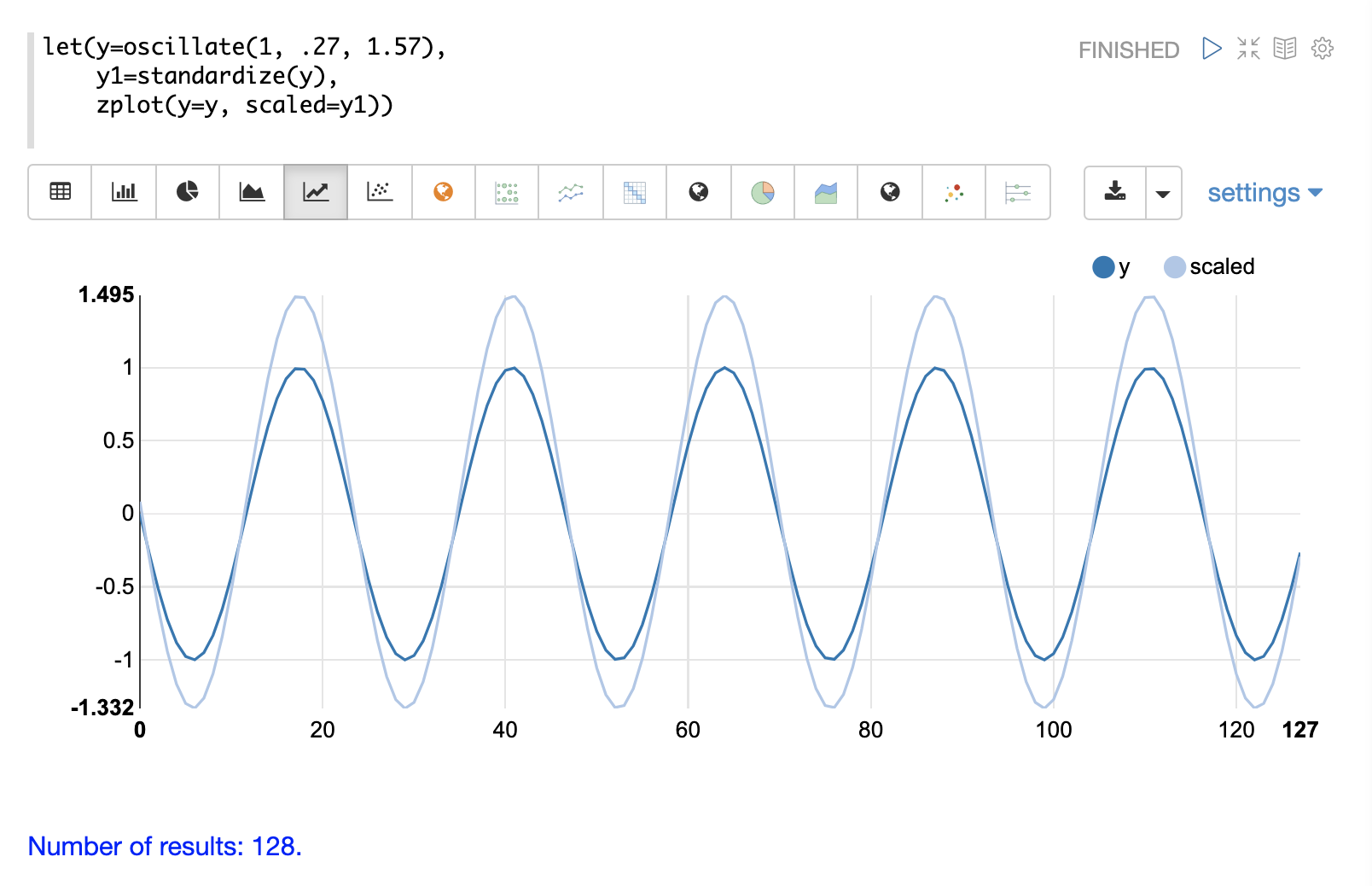
下面是一个标准化矩阵的简单示例。请注意,一旦将向量置于同一尺度,它们就相同了。
let(a=array(20, 30, 40, 50),
b=array(200, 300, 400, 500),
c=matrix(a, b),
d=standardize(c))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"d": [
[
-1.161895003862225,
-0.3872983346207417,
0.3872983346207417,
1.161895003862225
],
[
-1.1618950038622249,
-0.38729833462074165,
0.38729833462074165,
1.1618950038622249
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 17
}
]
}
}单位向量
unitize 函数将向量缩放为大小为 1。大小为 1 的向量称为单位向量。当向量数学处理向量方向而不是大小时,首选单位向量。
下面是正弦波的图,在单位化之前和之后,振幅为 1。
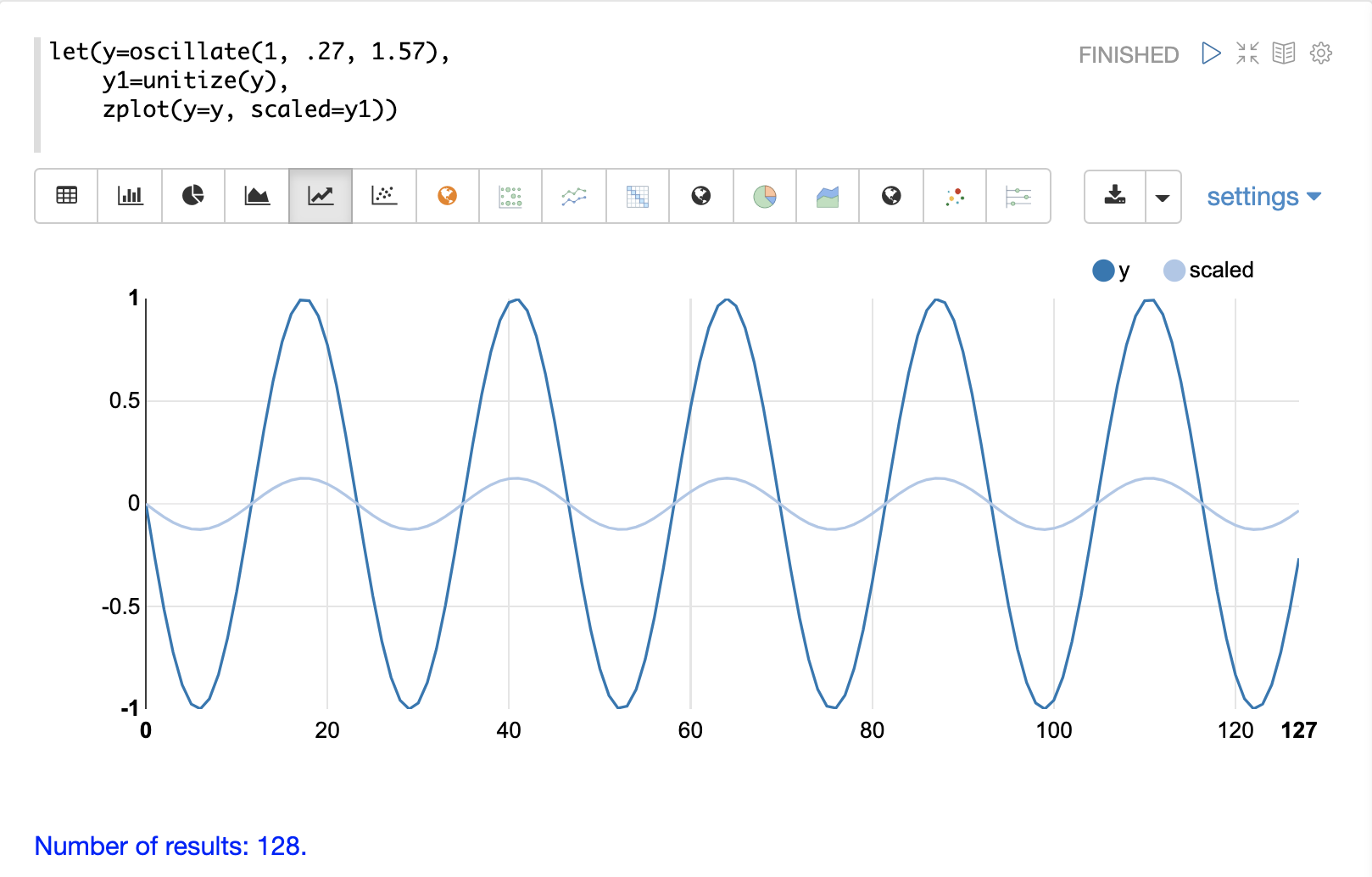
下面是一个单位化矩阵的简单示例。请注意,一旦将向量置于同一尺度,它们就相同了。
let(a=array(20, 30, 40, 50),
b=array(200, 300, 400, 500),
c=matrix(a, b),
d=unitize(c))当此表达式发送到 /stream 处理器时,它会响应
{
"result-set": {
"docs": [
{
"d": [
[
0.2721655269759087,
0.40824829046386296,
0.5443310539518174,
0.6804138174397716
],
[
0.2721655269759087,
0.4082482904638631,
0.5443310539518174,
0.6804138174397717
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 6
}
]
}
}