矩阵和矩阵数学

矩阵用作许多数学函数的输入和输出。本用户指南部分介绍了矩阵创建、操作和矩阵数学的基础知识。

矩阵

可以使用 matrix 函数创建矩阵。矩阵函数被传递一个 arrays 列表，其中每个数组代表矩阵中的一个行。

下面的示例创建一个二乘二的矩阵。

matrix(array(1, 2),
       array(4, 5))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "return-value": [
          [
            1,
            2
          ],
          [
            4,
            5
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }}

行和列标签

矩阵可以有列和行标签。可以使用函数 setRowLabels、setColumnLabels、getRowLabels 和 getColumnLabels 来设置和获取标签。标签值使用字符串数组设置。

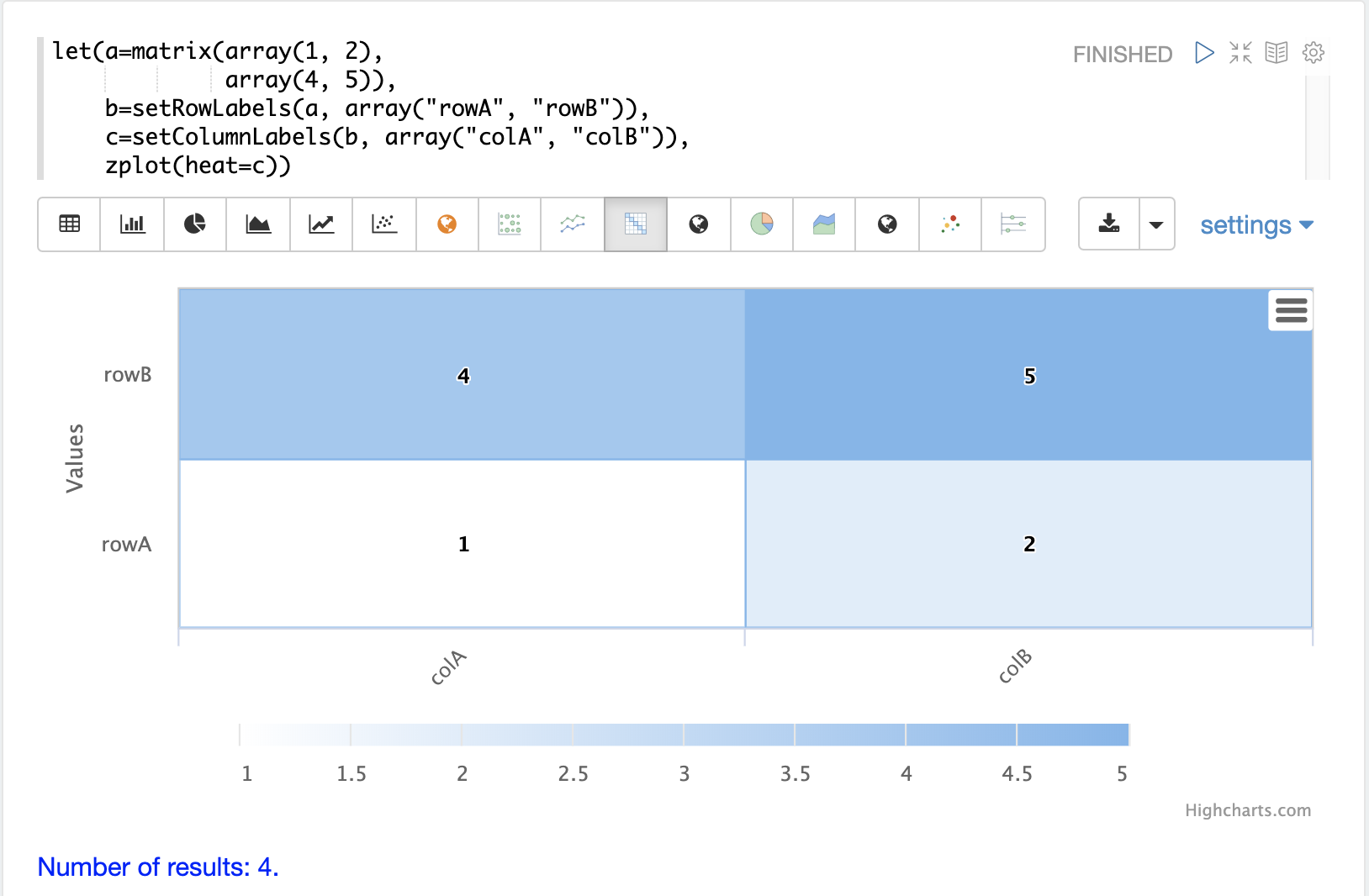
以下示例设置行和列标签。在用户指南的其他部分中，示例展示了函数如何返回已设置标签的矩阵。

下面是一个在矩阵上设置和获取行和列标签的简单示例。

let(echo="d, e",
    a=matrix(array(1, 2),
             array(4, 5)),
    b=setRowLabels(a, array("rowA", "rowB")),
    c=setColumnLabels(b, array("colA", "colB")),
    d=getRowLabels(c),
    e=getColumnLabels(c))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "d": [
          "rowA",
          "rowB"
        ],
        "e": [
          "colA",
          "colB"
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

可视化

zplot 函数可以使用 heat 命名参数将矩阵绘制为热图。热图是强大的可视化工具，用于显示指南后面描述的相关性和距离矩阵。下面的示例展示了使用 Apache Zeppelin 中的热图可视化方法可视化的 2x2 矩阵。

在下面的可视化中，行是从底部向上读取的，这是热图的通用约定。

$matrix$

访问行和列

可以使用 rowAt 和 colAt 函数访问矩阵的行和列。

以下示例创建一个 2x2 矩阵并返回矩阵的第二列。请注意，在此示例中，矩阵被传递了变量，而不是直接传递了数组列表。

let(a=array(1, 2),
    b=array(4, 5),
    c=matrix(a, b),
    d=colAt(c, 1))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "d": [
          2,
          5
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

矩阵属性

矩阵还可以具有与之关联的任意一组命名属性。某些函数（例如 termVectors 函数）返回包含描述矩阵中数据的属性的矩阵。

可以使用 getAttribute 函数按名称检索属性，并且可以使用 getAttributes 函数返回整个属性映射。

矩阵维度

可以使用 rowCount 和 columnCount 函数确定矩阵的维度。

以下示例检索矩阵的维度。

let(echo="b,c",
    a=matrix(array(1, 2, 3),
             array(4, 5, 6)),
    b=rowCount(a),
    c=columnCount(a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": 2,
        "c": 3
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

矩阵转置

可以使用 transpose 函数转置矩阵。

下面显示了矩阵转置的示例

let(a=matrix(array(1, 2),
             array(4, 5)),
    b=transpose(a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": [
          [
            1,
            4
          ],
          [
            2,
            5
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 24
      }
    ]
  }
}

矩阵求和

可以使用 sumRows 和 sumColumns 函数对矩阵的行和列求和。以下是 sumRows 函数的示例，该函数返回一个数组，其中包含每一行的总和。

let(a=matrix(array(1, 2, 3),
             array(4, 5, 6)),
    b=sumRows(a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": [
          6,
          15
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 2
      }
    ]
  }
}

grandSum 函数返回矩阵中所有值的总和。以下是 grandSum 函数的示例

let(a=matrix(array(1, 2, 3),
             array(4, 5, 6)),
    b=grandSum(a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": 21
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

标量矩阵运算

适用于向量的相同标量数学函数也适用于矩阵：scalarAdd、scalarSubtract、scalarMultiply、scalarDivide。

以下是 scalarAdd 函数的示例，该函数将标量值添加到矩阵中的每个元素。

let(a=matrix(array(1, 2),
             array(4, 5)),
    b=scalarAdd(10, a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": [
          [
            11,
            12
          ],
          [
            14,
            15
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

矩阵加法和减法

可以使用 ebeAdd 和 ebeSubtract 函数对两个矩阵进行加减运算，这两个函数执行矩阵的逐元素加法和减法。

以下是使用 ebeAdd 对矩阵自身进行逐元素相加的简单示例

let(a=matrix(array(1, 2),
             array(4, 5)),
    b=ebeAdd(a, a))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": [
          [
            2,
            4
          ],
          [
            8,
            10
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

矩阵乘法

可以使用 matrixMult 函数完成矩阵乘法。以下是矩阵乘法的简单示例

let(a=matrix(array(1, 2),
             array(4, 5)),
    b=matrix(array(11, 12),
             array(14, 15)),
    c=matrixMult(a, b))

当此表达式发送到 /stream 处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "c": [
          [
            39,
            42
          ],
          [
            114,
            123
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}